题目内容
(本小题满分12分)
函数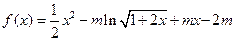 ,其中
,其中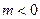 .
.
(Ⅰ)试讨论函数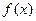 的单调性;
的单调性;
(Ⅱ)已知当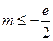 (其中
(其中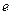 是自然对数的底数)时,在
是自然对数的底数)时,在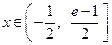 上至少
上至少
存在一点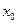 ,使
,使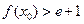 成立,求
成立,求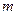 的取值范围;
的取值范围;
(Ⅲ)求证:当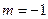 时,对任意
时,对任意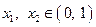 ,
,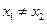 ,有
,有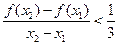 .
.
函数
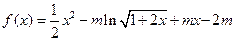 ,其中
,其中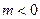 .
.(Ⅰ)试讨论函数
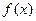 的单调性;
的单调性;(Ⅱ)已知当
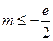 (其中
(其中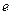 是自然对数的底数)时,在
是自然对数的底数)时,在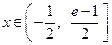 上至少
上至少存在一点
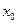 ,使
,使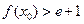 成立,求
成立,求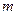 的取值范围;
的取值范围;(Ⅲ)求证:当
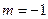 时,对任意
时,对任意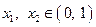 ,
,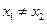 ,有
,有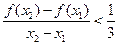 .
.(Ⅰ)见解析
(Ⅱ)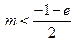
(Ⅲ)证明见解析。
(Ⅱ)
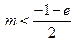
(Ⅲ)证明见解析。
(Ⅰ)易知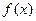 的定义域为
的定义域为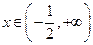 .
.
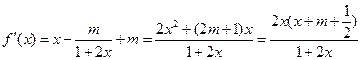 .
.
由 得:
得: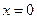 或
或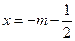 .
.
∵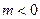 ,∴
,∴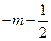
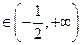 .
.
∴(1)当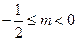 时,则
时,则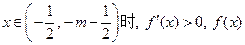 为增函数;
为增函数;
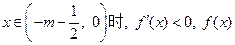 为减函数;
为减函数;
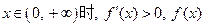 为增函数.
为增函数.
(2)当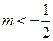 时,则
时,则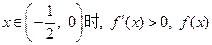 为增函数;
为增函数;
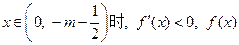 为减函数;
为减函数;
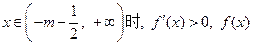 为增函数. 5分
为增函数. 5分
(Ⅱ)在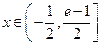 上至少存在一点
上至少存在一点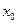 ,使
,使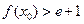 成立,等价于当
成立,等价于当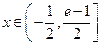 时,
时,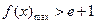 .
.
∵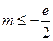 ,∴
,∴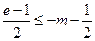 .
.
由(Ⅰ)知,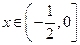 时,
时,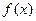 为增函数,
为增函数,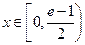 时,
时,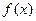 为减函数.
为减函数.
∴在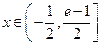 时,
时, .∴
.∴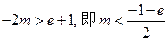 .
.
检验,上式满足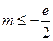 ,所以
,所以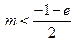 是所求范围. 8分
是所求范围. 8分
(Ⅲ)当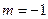 时,函数
时,函数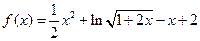 .构造辅助函数
.构造辅助函数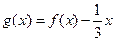 ,并求导得
,并求导得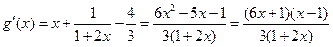 .
.
显然当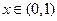 时,
时,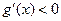 ,
,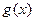 为减函数.
为减函数.
∴对任意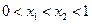 ,都有
,都有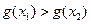 成立,即
成立,即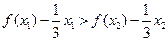 .
.
即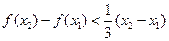 .又∵
.又∵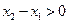 ,∴
,∴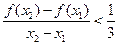 . 12分
. 12分
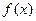 的定义域为
的定义域为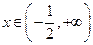 .
.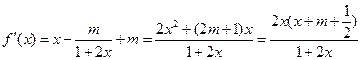 .
.由
 得:
得: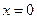 或
或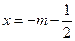 .
.∵
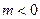 ,∴
,∴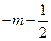
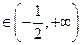 .
.∴(1)当
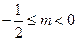 时,则
时,则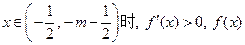 为增函数;
为增函数;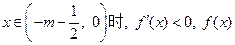 为减函数;
为减函数;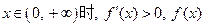 为增函数.
为增函数.(2)当
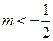 时,则
时,则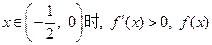 为增函数;
为增函数;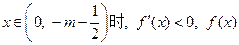 为减函数;
为减函数;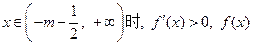 为增函数. 5分
为增函数. 5分(Ⅱ)在
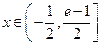 上至少存在一点
上至少存在一点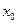 ,使
,使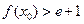 成立,等价于当
成立,等价于当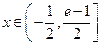 时,
时,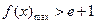 .
.∵
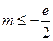 ,∴
,∴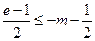 .
.由(Ⅰ)知,
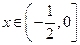 时,
时,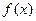 为增函数,
为增函数,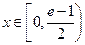 时,
时,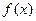 为减函数.
为减函数.∴在
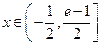 时,
时, .∴
.∴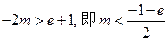 .
.检验,上式满足
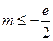 ,所以
,所以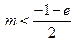 是所求范围. 8分
是所求范围. 8分(Ⅲ)当
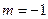 时,函数
时,函数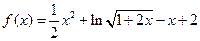 .构造辅助函数
.构造辅助函数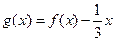 ,并求导得
,并求导得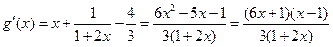 .
.显然当
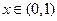 时,
时,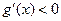 ,
,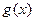 为减函数.
为减函数.∴对任意
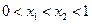 ,都有
,都有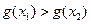 成立,即
成立,即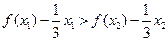 .
.即
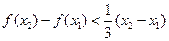 .又∵
.又∵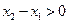 ,∴
,∴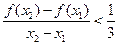 . 12分
. 12分
练习册系列答案
相关题目
 的函数
的函数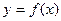 ,若同时满足下列条件:
,若同时满足下列条件: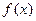 在
在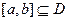 ,使
,使 上的值域为
上的值域为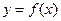
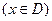 叫闭函数.
叫闭函数.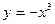 符合条件②的区间
符合条件②的区间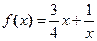 ,
,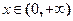 是否为闭函数?并说明理由;
是否为闭函数?并说明理由;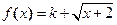 是闭函数,求实数
是闭函数,求实数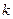 的范围?
的范围?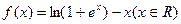 有下列性质:“若
有下列性质:“若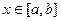 ,则存在
,则存在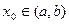 ,使得
,使得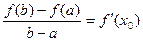 ”成立
”成立
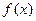 图象上三个不同的点,试判断△ABC的形状,并说明理由
图象上三个不同的点,试判断△ABC的形状,并说明理由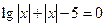 在区间
在区间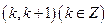 上有零点,则所有满足条件的
上有零点,则所有满足条件的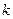 的值的和为 ______.
的值的和为 ______.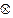 ”如下:当
”如下:当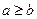 时,
时,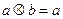 ;当
;当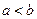 时,
时,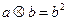 ,对于函数
,对于函数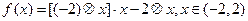 (“· ”和“
(“· ”和“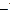 ”仍为通常的乘法和减法运算),把
”仍为通常的乘法和减法运算),把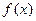 的图像按向量
的图像按向量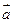 平移后得到
平移后得到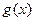 的图像,若
的图像,若 ____________.
____________.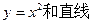
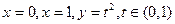 所围成的图形的面积的最小值是 。
所围成的图形的面积的最小值是 。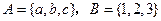 , 映射
, 映射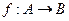 满足
满足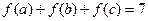 ,则这样的映射个数为( )
,则这样的映射个数为( )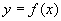 的定义域为R,当
的定义域为R,当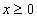 时,
时,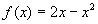 ,设函
,设函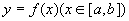 的值域为
的值域为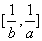 ,
,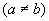 ,则b的最小值为_____________.
,则b的最小值为_____________.