题目内容
13.直三棱柱ABC-A1B1C1中,AB⊥BC,AB=BC=AA1=2,则该三棱柱的外接球的表面积为( )| A. | 4π | B. | 8π | C. | 12π | D. | $\frac{32π}{3}$ |
分析 根据题意判断直三棱柱ABC-A1B1C1的底面ABC为等腰直角三角形,我们可以把直三棱柱ABC-A1B1C1补成正四棱柱,则正四棱柱的体对角线是其外接球的直径,求出外接球的直径后,代入外接球的表面积公式,即可求出该三棱柱的外接球的表面积
解答 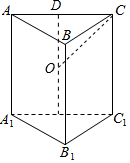 解:∵在直三棱锥ABC-A1B1C1中,AB⊥CB1,AB=BC=2,AA1=2,
解:∵在直三棱锥ABC-A1B1C1中,AB⊥CB1,AB=BC=2,AA1=2,
∴AB⊥面BCC1B1,
即AB⊥BC
∴直三棱柱ABC-A1B1C1的底面ABC为等腰直角三角形,
把直三棱柱ABC-A1B1C1补成正四棱柱,
则正四棱柱的体对角线是其外接球的直径,
设D,D1分别为AC,A1C1的中点,则DD1的中点O为球心,球的半径$R=\sqrt{C{D^2}+O{D^2}}=\sqrt{3}$,故表面积为S=4πR2=12π.
故选:C.
点评 在求一个几何体的外接球表面积(或体积)时,关键是求出外接球的半径,我们通常有如下办法:①构造三角形,解三角形求出R;②找出几何体上到各顶点距离相等的点,即球心,进而求出R;③将几何体补成一个长方体,其对角线即为球的直径,进而求出R

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
20.若实数x,y满足不等式组$\left\{\begin{array}{l}x-2y+2≥0\\ x+2y+2≥0\\ 2x-y-1≤0\end{array}\right.$,则2|x+1|+y的最大值是( )
| A. | $\frac{14}{3}$ | B. | $\frac{19}{3}$ | C. | 4 | D. | 1 |
5.在△ABC中,a=3,b=5,$cosA=\frac{{2\sqrt{2}}}{3}$,则sinB=( )
| A. | $\frac{1}{5}$ | B. | $\frac{5}{9}$ | C. | $\frac{{\sqrt{5}}}{3}$ | D. | 1 |
2.已知点M(ρ,θ),则M点关于极点对称的点N的极坐标是( )
| A. | (ρ,π+θ) | B. | (ρ,-θ) | C. | (ρ,π-θ) | D. | (ρ,2π-θ) |