题目内容
设函数f(x)=(sinωx+cosωx)2+2cos2ωx(ω>0)的最小正周期为 .
.
(1)求ω的值;
(2)当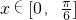 时,求f(x)的最值.
时,求f(x)的最值.
(3)若函数y=g(x)的图象是由y=f(x)的图象向右平移 个单位长度得到,求y=g(x)的单调增区间.
个单位长度得到,求y=g(x)的单调增区间.
解:(1)因为函数f(x)=(sinωx+cosωx)2+2cos2ωx
= ,
,
它的最小正周期为 .
.
 ,
,
所以 …(4分)
…(4分)
(2)因为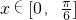
所以 …(5分)
…(5分)
 …(6分)
…(6分)
当 ,即
,即 时,
时, ,
,
当 ,即
,即 时,ymin=3…(8分)
时,ymin=3…(8分)
(3)f(x)= ,
,
的图象向右平移 个单位长度得到
个单位长度得到 …(10分)
…(10分)

单调增区间是 …(12分)
…(12分)
分析:(1)通过三角函数的基本关系式与二倍角公式,把函数化简为 一个角的一个三角函数的形式,通过周期求出ω的值.
(2)当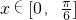 时,
时, ,然后求出f(x)的最值.
,然后求出f(x)的最值.
(3)由y=f(x)的图象向右平移 个单位长度得到y=g(x)的表达式,利用正弦函数的单调增区间求出函数的单调增区间.
个单位长度得到y=g(x)的表达式,利用正弦函数的单调增区间求出函数的单调增区间.
点评:本题是中档题,考查三角函数的化简求值,周期的应用,三角函数的最值,单调增区间的求法,考查计算能力,常考题型.
=
 ,
,它的最小正周期为
 .
. ,
,所以
 …(4分)
…(4分)(2)因为
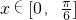
所以
 …(5分)
…(5分) …(6分)
…(6分)当
 ,即
,即 时,
时, ,
,当
 ,即
,即 时,ymin=3…(8分)
时,ymin=3…(8分)(3)f(x)=
 ,
,的图象向右平移
 个单位长度得到
个单位长度得到 …(10分)
…(10分)
单调增区间是
 …(12分)
…(12分)分析:(1)通过三角函数的基本关系式与二倍角公式,把函数化简为 一个角的一个三角函数的形式,通过周期求出ω的值.
(2)当
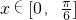 时,
时, ,然后求出f(x)的最值.
,然后求出f(x)的最值.(3)由y=f(x)的图象向右平移
 个单位长度得到y=g(x)的表达式,利用正弦函数的单调增区间求出函数的单调增区间.
个单位长度得到y=g(x)的表达式,利用正弦函数的单调增区间求出函数的单调增区间.点评:本题是中档题,考查三角函数的化简求值,周期的应用,三角函数的最值,单调增区间的求法,考查计算能力,常考题型.

练习册系列答案
相关题目