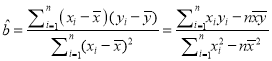题目内容
【题目】已知函数f(x)=sin(x﹣φ),且 ![]() f(x)dx=0,则函数f(x)的图象的一条对称轴是( )
f(x)dx=0,则函数f(x)的图象的一条对称轴是( )
A.x= ![]()
B.x= ![]()
C.x= ![]()
D.x= ![]()
【答案】A
【解析】解:∵函数f(x)=sin(x﹣φ), ![]() f(x)dx=﹣cos(x﹣φ)
f(x)dx=﹣cos(x﹣φ) ![]() =﹣cos(
=﹣cos( ![]() ﹣φ)﹣[﹣cos(﹣φ)]=
﹣φ)﹣[﹣cos(﹣φ)]= ![]() cosφ﹣
cosφ﹣ ![]() sinφ=
sinφ= ![]() cos(φ+
cos(φ+ ![]() )=0,
)=0,
∴φ+ ![]() =kπ+
=kπ+ ![]() ,k∈z,即 φ=kπ+
,k∈z,即 φ=kπ+ ![]() ,k∈z,故可取φ=
,k∈z,故可取φ= ![]() ,f(x)=sin(x﹣
,f(x)=sin(x﹣ ![]() ).
).
令x﹣ ![]() =kπ+
=kπ+ ![]() ,求得 x=kπ+
,求得 x=kπ+ ![]() ,k∈Z,
,k∈Z,
则函数f(x)的图象的一条对称轴为 x= ![]() ,
,
故选:A.
由 ![]() f(x)dx=0求得
f(x)dx=0求得 ![]() cos(φ+
cos(φ+ ![]() )=0,故有 φ+
)=0,故有 φ+ ![]() =kπ+
=kπ+ ![]() ,k∈z.可取φ=
,k∈z.可取φ= ![]() ,则f(x)=sin(x﹣
,则f(x)=sin(x﹣ ![]() ).
).
令x﹣ ![]() =kπ+
=kπ+ ![]() ,求得x的值,可得函数f(x)的图象的一条对称轴方程.
,求得x的值,可得函数f(x)的图象的一条对称轴方程.

练习册系列答案
相关题目
【题目】某产品的广告费用x与销售额y的统计数据如表:
广告费用x(万元) | 4 | 2 | 3 | 5 |
销售额y(万元) | 49 | 26 | 39 | 54 |
根据上表可得回归方程 ![]() =
= ![]() x+
x+ ![]() 中的
中的 ![]() 为9.4,据此模型预报广告费用为6万元时销售额为( )
为9.4,据此模型预报广告费用为6万元时销售额为( )
A.63.6万元
B.67.7万元
C.65.5万元
D.72.0万元