题目内容
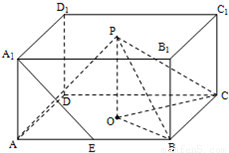
如图,P、O分别是正四棱柱ABCD-A1B1C1D1上、下底面的中心,AB=kAA1.(1)当
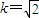 时,求直线PA与平面PBC所成角的大小;
时,求直线PA与平面PBC所成角的大小;(2)当k取何值时,O在平面PBC内的射影恰好为△PBC的重心?

【答案】分析:以点O为原点,直线OA、OB、OP所在直线分别为x、y、z轴,建立如图所示的空间直角坐标系,不妨设 ,
,
(1)求出对应各点的坐标,设出平面PBC的法向量为 ,,并求出平面PBC的法向量,再根据
,,并求出平面PBC的法向量,再根据 =
= ,即可得到直线PA与平面PBC所成角的大小;
,即可得到直线PA与平面PBC所成角的大小;
(2)先由(Ⅰ)知△PBC的重心G为 ,再根据
,再根据 ,解得k的值即可.
,解得k的值即可.
解答: 解:以点O为原点,直线OA、OB、OP所在直线分别为x、y、z轴,建立如图所示的空间直角坐标系,不妨设
解:以点O为原点,直线OA、OB、OP所在直线分别为x、y、z轴,建立如图所示的空间直角坐标系,不妨设 ,则得
,则得 、
、 、B(0,2,0)、C(-2,0,0)
、B(0,2,0)、C(-2,0,0)
_
(1)当 时,由P(0,0,2)、A(2,0,0)得
时,由P(0,0,2)、A(2,0,0)得 、
、 、
、
设平面PBC的法向量为 ,则由
,则由 ,得
,得 ,
,
∴
 =
= ,
,
∴直线PA与平面PBC所成角的大小为 .
.
(2)由(Ⅰ)知△PBC的重心G为 ,则
,则 ,
,
若O在平面PBC内的射影恰好为△PBC的重心,则有 ,解得
,解得
∴当 时,O在平面PBC内的射影恰好为△PBC的重心.
时,O在平面PBC内的射影恰好为△PBC的重心.
点评:本题是中档题,考查空间向量求直线与平面的夹角,法向量的求法,直线与平面所成的角,考查计算能力.
 ,
,(1)求出对应各点的坐标,设出平面PBC的法向量为
 ,,并求出平面PBC的法向量,再根据
,,并求出平面PBC的法向量,再根据 =
= ,即可得到直线PA与平面PBC所成角的大小;
,即可得到直线PA与平面PBC所成角的大小;(2)先由(Ⅰ)知△PBC的重心G为
 ,再根据
,再根据 ,解得k的值即可.
,解得k的值即可.解答:
 解:以点O为原点,直线OA、OB、OP所在直线分别为x、y、z轴,建立如图所示的空间直角坐标系,不妨设
解:以点O为原点,直线OA、OB、OP所在直线分别为x、y、z轴,建立如图所示的空间直角坐标系,不妨设 ,则得
,则得 、
、 、B(0,2,0)、C(-2,0,0)
、B(0,2,0)、C(-2,0,0)_
(1)当
 时,由P(0,0,2)、A(2,0,0)得
时,由P(0,0,2)、A(2,0,0)得 、
、 、
、
设平面PBC的法向量为
 ,则由
,则由 ,得
,得 ,
,
∴

 =
= ,
,∴直线PA与平面PBC所成角的大小为
 .
.(2)由(Ⅰ)知△PBC的重心G为
 ,则
,则 ,
,若O在平面PBC内的射影恰好为△PBC的重心,则有
 ,解得
,解得
∴当
 时,O在平面PBC内的射影恰好为△PBC的重心.
时,O在平面PBC内的射影恰好为△PBC的重心.点评:本题是中档题,考查空间向量求直线与平面的夹角,法向量的求法,直线与平面所成的角,考查计算能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
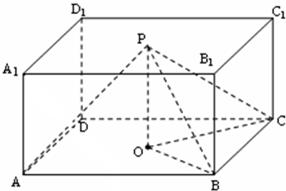 如图,P、O分别是正四棱柱ABCD-A1B1C1D1上、下底面的中心,AB=kAA1.
如图,P、O分别是正四棱柱ABCD-A1B1C1D1上、下底面的中心,AB=kAA1. 如图,已知P、O分别是正四棱柱ABCD-A1B1C1D1上、下底面的中心,E是AB的中点,AB=kAA1,其中k为非零实数,
如图,已知P、O分别是正四棱柱ABCD-A1B1C1D1上、下底面的中心,E是AB的中点,AB=kAA1,其中k为非零实数, 如图,在正四棱锥S-ABCD中,AB=
如图,在正四棱锥S-ABCD中,AB=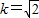 时,求直线PA与平面PBC所成角的正弦值;
时,求直线PA与平面PBC所成角的正弦值;