题目内容
 如图,△VAC中,VC⊥AC,将其绕直线VC旋转得到△VBC,D是AB的中点,AB=
如图,△VAC中,VC⊥AC,将其绕直线VC旋转得到△VBC,D是AB的中点,AB=| 2 |
| π |
| 2 |
(Ⅰ)求证:平面VAB⊥平面VCD;
(Ⅱ)当角θ变化时,求直线BC与平面VAB所成的角的取值范围.
(Ⅲ)θ=
| π |
| 4 |
| π |
| 4 |
| BE |
| BV |
分析:(I)根据已知中,△VAC中,VC⊥AC,将其绕直线VC旋转得到△VBC,D是AB的中点,我们易得到VC⊥AC,VC⊥BC,进而根据线面垂直的判定定理,得到平面VAB⊥平面VCD;,以C为坐标原点,CA、CB、CV为x、y、z轴建立坐标系如图,我们求出各顶点的坐标,进而确定直线AB与平面VCD的法向量,利用向量法证明,AB⊥平面VCD,再由面垂直的判定定理得到平面VAB⊥平面VCD;
(Ⅱ)设平面VAB的法向量为
=(x,y,z),并求出平面VAB的法向量
,并设直线BC与平面VAB所成角为φ,根据已知中AB=
a,AC=a,∠VDC=θ(0<θ<
),结合向量夹角公式,易得到直线BC与平面VAB所成的角的取值范围.
(III)当θ=
时,则我们易求出满足条件的V点的坐标,进而求出满足条件的E点坐标,根据二面角E-CD-B的大小也为
,我们易构造一个关于λ方程,解方程即可求出满足条件的λ.
(Ⅱ)设平面VAB的法向量为
| n |
| n |
| 2 |
| π |
| 2 |
(III)当θ=
| π |
| 4 |
| π |
| 4 |
解答:解:(Ⅰ)∵AB=
a,AC=BC=a,
∴AC⊥BC,
∵VC⊥AC,VC⊥BC,
∴VC⊥平面ABC,
以C为坐标原点,CA、CB、CV为x、y、z轴建立坐标系如图,
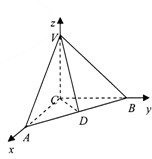
则A(a,0,0),B(0,a,0),D(
,
,0),V(0,0,
tanθ ),
∴
=(
,
,-
tanθ ),
=(
,
,0),
=(-a,a,0),
∴
•
=0,
•
=0,
∴AB⊥平面VCD,
∵AB?平面VAB,
∴平面VAB⊥平面VCD.
(Ⅱ)设平面VAB的法向量为
=(x,y,z),
∴
•
=0,
•
=0,
∴
,
∴又
=(1,1,
),
又∵
=(0,-a,0)
设直线BC与平面VAB所成角为φ,
∴sinφ=|
|=
sinθ,
∵0<θ<
,∴0<sinθ<1,0<sinφ<
0≤φ≤
,∴0<φ<
.λ
(Ⅲ)当θ=
时,V点坐标为(0,0,
a),
假设存在点E,则
=λ
,
∴E点坐标为( 0,(1-λ)a,
λa)
设平面CDE的法向量为
=(x,y,z)
∴
•
=0,
•
=0
∴
,
∴
=(1,-1,
)
∵二面角E-CD-B的大小为
,
∴cos
=
=
,
∴
=1,
∴λ=
,
故符合题意的λ=
.
| 2 |
∴AC⊥BC,
∵VC⊥AC,VC⊥BC,
∴VC⊥平面ABC,
以C为坐标原点,CA、CB、CV为x、y、z轴建立坐标系如图,

则A(a,0,0),B(0,a,0),D(
| a |
| 2 |
| a |
| 2 |
| ||
| 2 |
∴
| VD |
| a |
| 2 |
| a |
| 2 |
| ||
| 2 |
| CD |
| a |
| 2 |
| a |
| 2 |
| AB |
∴
| AB |
| CD |
| AB |
| VD |
∴AB⊥平面VCD,
∵AB?平面VAB,
∴平面VAB⊥平面VCD.
(Ⅱ)设平面VAB的法向量为
| n |
∴
| n |
| AB |
| n |
| VD |
∴
|
∴又
| n |
| ||
| tanθ |
又∵
| BC |
设直线BC与平面VAB所成角为φ,
∴sinφ=|
| ||||
|
|
| ||
| 2 |
∵0<θ<
| π |
| 2 |
| ||
| 2 |
0≤φ≤
| π |
| 2 |
| π |
| 4 |
(Ⅲ)当θ=
| π |
| 4 |
| ||
| 2 |
假设存在点E,则
| BE |
| BV |
∴E点坐标为( 0,(1-λ)a,
| ||
| 2 |
设平面CDE的法向量为
| m |
∴
| m |
| CE |
| m |
| CD |
∴
|
∴
| m |
| ||
| λ |
∵二面角E-CD-B的大小为
| π |
| 4 |
∴cos
| π |
| 4 |
| ||||
|
|
| ||
| 2 |
∴
| 1-λ |
| λ |
∴λ=
| 1 |
| 2 |
故符合题意的λ=
| 1 |
| 2 |
点评:本题考查的知识点是平面与平面垂直的判定,直线与平面所成的角,其中建立空间坐标系,将面面垂直的证明及直线与平面的夹角均转化为向量夹角问题是解答本题的关键.

练习册系列答案
 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
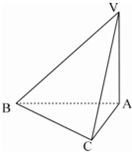 如图,已知三棱锥V-ABC中,∠VAB=∠VAC=∠ABC=90°且BC=1,AC=2,VA=2.
如图,已知三棱锥V-ABC中,∠VAB=∠VAC=∠ABC=90°且BC=1,AC=2,VA=2. ,且BC=a,AB=b,AV=c,求:
,且BC=a,AB=b,AV=c,求:
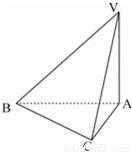 如图,已知三棱锥V-ABC中,∠VAB=∠VAC=∠ABC=90°且BC=1,AC=2,VA=2.
如图,已知三棱锥V-ABC中,∠VAB=∠VAC=∠ABC=90°且BC=1,AC=2,VA=2.