Question

已知{a_n}是各项不为0的等差数列，S_n为其前n项和，且a_n²=S_2n-1，n∈N^*．
（1）求a_n；
（2）设数列{b_n}满足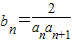，T_n为数列{b_n}的前n项和．
（ⅰ）求T_n；
（ⅱ）若对任意的n∈N^*，不等式λT_n＜n+8•（-1）ⁿ恒成立，求实数λ的取值范围．

Answer 1

【答案】分析：（1）设公差为d，在a_n²=S_2n-1中，令n=1，n=2，可得关于a₁，d的方程组，解出a₁，d，由等差数列通项公式可得a_n；
（2）（i）b_n==），利用裂项相消法可求得T_n；
（ii）分n为偶数，n为奇数两种情况进行讨论：分别分离出参数λ后，转化为最值问题解决，分别利用基本不等式、单调性可求得最值；
解答：解：（1）设公差为d，在a_n²=S_2n-1中，令n=1，n=2，
得，即，解得a₁=1，d=2，
∴a_n=2n-1．
（2）（i）．∵b_n==），
∴T_n=（1-）（-）+…+（）=1-=．
（ii））①当n为偶数时，要使不等式λT_n＜n+8•（-1）ⁿ恒成立，即需不等式λ＜=n++恒成立．
∵n+≥4，等号在n=2时取得．∴此时λ需满足λ＜．
②当n为奇数时，要使不等式λT_n＜n+8•（-1）ⁿ恒成立，即需不等式λ＜=n--恒成立．
∵n-是随n的增大而增大，∴n=1时n-取得最小值-3，
∴此时λ需满足λ＜-．
综合①、②可得λ的取值范围是λ＜-．
点评：本题考查由数列递推式求数列通项、数列求和，恒成立问题，考查转化思想、分类讨论思想，考查学生分析解决问题的能力．