题目内容
已知向量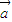 =(cosα,sinα),
=(cosα,sinα),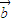 =(cosx,sinx),
=(cosx,sinx),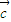 =(sinx+2sinα,cosx+2cosα),其中0<α<x<π.
=(sinx+2sinα,cosx+2cosα),其中0<α<x<π.(1)若
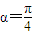 ,求函数f(x)=
,求函数f(x)=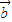 •
•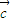 的最小值及相应x的值;
的最小值及相应x的值;(2)若
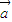 与
与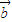 的夹角为
的夹角为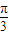 ,且
,且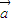 ⊥
⊥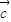 ,求tan2α的值.
,求tan2α的值.
【答案】分析:(1)根据向量点乘表示出函数f(x)的解析式后令t=sinx+cosx转化为二次函数解题.
(2)根据向量a与b的夹角为 确定
确定 ,再由a⊥c可知向量a点乘向量c等于0整理可得sin(x+α)+2sin2α=0,再将
,再由a⊥c可知向量a点乘向量c等于0整理可得sin(x+α)+2sin2α=0,再将 代入即可得到答案.
代入即可得到答案.
解答:解:(1)∵ =(cosx,sinx),
=(cosx,sinx),
 =(sinx+2sinα,cosx+2cosα),
=(sinx+2sinα,cosx+2cosα), ,
,
∴f(x)= •
• =cosxsinx+2cosxsinα+sinxcosx+2sinxcosα=
=cosxsinx+2cosxsinα+sinxcosx+2sinxcosα= .
.
令t=sinx+cosx(0<x<π),
则2sinxcosx=t2-1,且 .
.
则 ,
, .
.
∴ 时,
时, ,此时
,此时 .
.
由于0<x<π,故 .
.
所以函数f(x)的最小值为 ,相应x的值为
,相应x的值为 ;
;
(2)∵ 与
与 的夹角为
的夹角为 ,
,
∴ .
.
∵0<α<x<π,∴0<x-α<π,∴ .
.
∵ ⊥
⊥ ,∴cosα(sinx+2sinα)+sinα(cosx+2cosα)=0.
,∴cosα(sinx+2sinα)+sinα(cosx+2cosα)=0.
∴sin(x+α)+2sin2α=0, .
.
∴ ,
,
∴ .
.
点评:本题主要考查平面向量的坐标运算和数量积运算.向量一般和三角函数放在一起进行考查,这种题型是高考的热点,每年必考.
(2)根据向量a与b的夹角为
 确定
确定 ,再由a⊥c可知向量a点乘向量c等于0整理可得sin(x+α)+2sin2α=0,再将
,再由a⊥c可知向量a点乘向量c等于0整理可得sin(x+α)+2sin2α=0,再将 代入即可得到答案.
代入即可得到答案.解答:解:(1)∵
 =(cosx,sinx),
=(cosx,sinx), =(sinx+2sinα,cosx+2cosα),
=(sinx+2sinα,cosx+2cosα), ,
,∴f(x)=
 •
• =cosxsinx+2cosxsinα+sinxcosx+2sinxcosα=
=cosxsinx+2cosxsinα+sinxcosx+2sinxcosα= .
.令t=sinx+cosx(0<x<π),
则2sinxcosx=t2-1,且
 .
.则
 ,
, .
.∴
 时,
时, ,此时
,此时 .
.由于0<x<π,故
 .
.所以函数f(x)的最小值为
 ,相应x的值为
,相应x的值为 ;
;(2)∵
 与
与 的夹角为
的夹角为 ,
,∴
 .
.∵0<α<x<π,∴0<x-α<π,∴
 .
.∵
 ⊥
⊥ ,∴cosα(sinx+2sinα)+sinα(cosx+2cosα)=0.
,∴cosα(sinx+2sinα)+sinα(cosx+2cosα)=0.∴sin(x+α)+2sin2α=0,
 .
.∴
 ,
,∴
 .
.点评:本题主要考查平面向量的坐标运算和数量积运算.向量一般和三角函数放在一起进行考查,这种题型是高考的热点,每年必考.

练习册系列答案
相关题目
已知向量
=(cosα,sinα),
=(cosβ,sinβ),若|
-
|=
,则
和
的夹角为( )
| a |
| b |
| a |
| b |
| 2 |
| a |
| b |
| A、60° | B、90° |
| C、120° | D、150° |