题目内容
如图已知每条棱长都为3的直平行六面体ABCD-A1B1C1D1中,∠BAD=60°,长为2的线段MN的一个端点M在DD1上运动,另一个端点N在底面ABCD上运动,则MN中点P的轨迹与直平行六面体的面所围成的几何体的体积为______.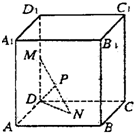


取AB的中点E连接DE,由题意知DE⊥AB,DE⊥CD
以DE所在直线为x轴,以DC所在直线为y轴,以DD1所在直线为z轴建立如图空间直角坐标系
设M(0,0,z),N(x,y,0),则P(
| x |
| 2 |
| y |
| 2 |
| z |
| 2 |
MN=
| x2+y2+z2 |
∴x2+y2+z2=4
∴
| x2 |
| 4 |
| y2 |
| 4 |
| z2 |
| 4 |
| x |
| 2 |
| y |
| 2 |
| z |
| 2 |
∴OP2=1
即OP=1
∴点P的轨迹是以原点D为球心,以1为半径的球的一部分
又∵∠BAD=60°
∴∠ADC=120°
∴点P的轨迹是球的
| 1 |
| 6 |
∴几何体的体积为V=
| 1 |
| 6 |
| 4 |
| 3 |
| 2π |
| 9 |
故答案为:
| 2π |
| 9 |

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
 如图已知每条棱长都为3的直平行六面体ABCD-A1B1C1D1中,∠BAD=60°,长为2的线段MN的一个端点M在DD1上运动,另一个端点N在底面ABCD上运动,则MN中点P的轨迹与直平行六面体的面所围成的几何体的体积为
如图已知每条棱长都为3的直平行六面体ABCD-A1B1C1D1中,∠BAD=60°,长为2的线段MN的一个端点M在DD1上运动,另一个端点N在底面ABCD上运动,则MN中点P的轨迹与直平行六面体的面所围成的几何体的体积为 如图已知每条棱长都为3的直平行六面体ABCD-A1B1C1D1中,∠BAD=60°,长为2的线段MN的一个端点M在DD1上运动,另一个端点N在底面ABCD上运动,则MN中点P的轨迹与直平行六面体的面所围成的几何体的体积为________.
如图已知每条棱长都为3的直平行六面体ABCD-A1B1C1D1中,∠BAD=60°,长为2的线段MN的一个端点M在DD1上运动,另一个端点N在底面ABCD上运动,则MN中点P的轨迹与直平行六面体的面所围成的几何体的体积为________.
