题目内容
四棱锥S-ABCD的底面为正方形,SD⊥底面ABCD,如下列结论中不正确的是.( )
分析:利用三垂线定理可得选项A正确,利用线面垂直的判定定理可得选项B正确,根据直线和平面所成的角的定义和求法,可得选项C不正确,选项D正确,从而得出结论.
解答:解:由于ABCD 为正方形,SD⊥底面ABCD,故AD是SA在底面ABCD内的射影,再由正方形ABCD中,AB⊥AD,可得AB⊥SA,故选项A正确.
由于正方形ABCD中,BC∥AD,AD?面ABCD,AC不在面ABCD 内,故有BC∥平面SAD,故选项B正确.
由于正方形ABCD中,BC∥AD,故锐角∠SAD即为BC与SA所成的角.由于AD⊥平面SDC,故BC⊥平面SDC,而SC在平面SDC内,故有AD⊥SC,
故BC与SA所成的角不等于AD与SC所成的角,故选项C不正确.
设AC与BD的交点为O,则由题意可得AC垂直于平面SBD,SA与平面SBD成的角为∠ASO,SC与平面SBD成的角为∠CSO,AO=SO.
由于tan∠ASO=
,tan∠ASO=
,故tan∠ASO=tan∠ASO,故有∠ASO=∠ASO,故选项D正确.
故选C.
由于正方形ABCD中,BC∥AD,AD?面ABCD,AC不在面ABCD 内,故有BC∥平面SAD,故选项B正确.
由于正方形ABCD中,BC∥AD,故锐角∠SAD即为BC与SA所成的角.由于AD⊥平面SDC,故BC⊥平面SDC,而SC在平面SDC内,故有AD⊥SC,
故BC与SA所成的角不等于AD与SC所成的角,故选项C不正确.
设AC与BD的交点为O,则由题意可得AC垂直于平面SBD,SA与平面SBD成的角为∠ASO,SC与平面SBD成的角为∠CSO,AO=SO.
由于tan∠ASO=
| AO |
| SO |
| CO |
| SO |
故选C.
点评:本题主要考查棱锥的结构特征,空间角与空间位置关系的确定,属于基础题.

练习册系列答案
相关题目
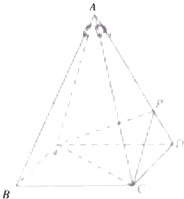 如图,四棱锥S-ABCD的底面是正方形,每条侧棱的长都是底面边长的
如图,四棱锥S-ABCD的底面是正方形,每条侧棱的长都是底面边长的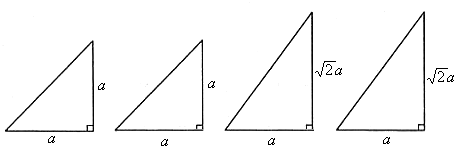
 (2012•黄浦区一模)已知四棱锥S-ABCD的底面ABCD是直角梯形,AB∥CD,BC⊥AB,侧面SAB为正三角形,AB=BC=4,CD=SD=2.如图所示.
(2012•黄浦区一模)已知四棱锥S-ABCD的底面ABCD是直角梯形,AB∥CD,BC⊥AB,侧面SAB为正三角形,AB=BC=4,CD=SD=2.如图所示. 如图已知四棱锥S-ABCD的底面是直角梯形,AB∥DC,∠DAB=90°,SA⊥底面ABCD,且SA=AD=DC=
如图已知四棱锥S-ABCD的底面是直角梯形,AB∥DC,∠DAB=90°,SA⊥底面ABCD,且SA=AD=DC=