题目内容

在抛物线y2=2x上求一点P，使P到焦点F与到点A（3，2）的距离之和最小.

解：如图，设抛物线上的点P到准线的距离为|PQ|.

由抛物线定义可知：

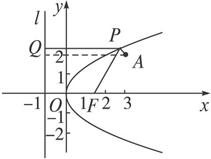
|PF|+|PA|=|PQ|+|PA|，显然当P、Q、A三点共线时，

|PQ|+|PA|最小.

∵A（3，2），将y=2代入y2=2x,得x=2,∴P点坐标（2，2）。

练习册系列答案
相关题目
已知正三角形OAB的三个顶点都在抛物线y2=2x上，其中O为坐标原点，设圆C是OAB的内接圆（点C为圆心）
（Ⅰ）求圆C的方程；
（Ⅱ）设圆M的方程为（x-4-7cosθ）2+（y-7cosθ）2=1，过圆M上任意一点P分别作圆C的两条切线PE，PF，切点为E，F，求
CE
•
CF
的最大值和最小值．
已知点P在直线x+y+5=0上，点Q在抛物线y2=2x上，则|PQ|的最小值等于
 
．
（文）圆心在抛物线y2=2x上，且与该抛物线的准线和x轴都相切的圆的方程是（　　）
A、(x-
1
2
)2+(y-1)2=1
B、(x-
1
2
)2+(y±1)2=1
C、(x-
1
2
)2+(y±
1
2
)2=
1
4
D、(x-
1
2
)2+(y+1)2=1
已知点A在抛物线y2=2x上，且到焦点F与到点B（2，1）的距离之和最小，则点A的坐标为
(
1
2
，1)
(
1
2
，1)
．
已知定点A（-3，0），B（3，0），动点P在抛物线y2=2x上的移动，则
PA
•
PB
的最小值等于
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网