题目内容
设有一颗彗星沿一椭圆轨道绕地球运行,地球恰好位于椭圆轨道的焦点处,当此彗星离地球相距m万千米和
剖析:本题的实际意义是求椭圆上一点到焦点的距离,一般的思路:由直线与椭圆的关系,列方程组解之;或利用定义法抓住椭圆的第二定义求解.同时,还要注意结合椭圆的几何意义进行思考.仔细分析题意,由椭圆的几何意义可知:只有当该彗星运行到椭圆的较近顶点处时,彗星与地球的距离才达到最小值即为a-c,这样把问题就转化为求a、c或a-c.
解:建立如下图所示直角坐标系,设地球位于焦点F(-c,0)处,椭圆的方程为![]() +
+![]() =1,
=1,

当过地球和彗星的直线与椭圆的长轴夹角为π3时,由椭圆的几何意义可知,彗星A只能满足∠xFA=![]() (或∠xFA′=
(或∠xFA′=![]() ).
).
作AB⊥Ox于B,则|FB|=![]() |FA|=
|FA|=![]() m,
m,
故由椭圆的第二定义可得
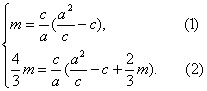
两式相减得![]() m=
m=![]() ·
·![]() m,∴a=2c.
m,∴a=2c.
代入①,得m=![]() (4c-c)=
(4c-c)=![]() c,
c,
∴c=![]() m.
m.
∴a-c=c=![]() m.
m.
答:彗星与地球的最近距离为![]() m万千米.
m万千米.
讲评:(1)在天体运行中,彗星绕恒星运行的轨道一般都是椭圆,而恒星正是它的一个焦点,该椭圆的两个端点,一个是近地点,另一个则是远地点,这两点到恒星的距离一个是a-c,另一个是a+c.
(2)以上给出的解答是建立在椭圆的概念和几何意义之上的,以数学概念为根基充分体现了数形结合的思想.另外,数学应用问题的解决在数学化的过程中也要时刻不忘审题,善于挖掘隐含条件,有意识地训练数学思维品质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 m万千米时,经过地球和彗星的直线与椭圆的长轴夹角分别为
m万千米时,经过地球和彗星的直线与椭圆的长轴夹角分别为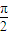 和
和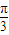 ,求该彗星与地球的最近距离.
,求该彗星与地球的最近距离.