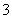题目内容
函数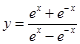 的图象大致为( ).
的图象大致为( ).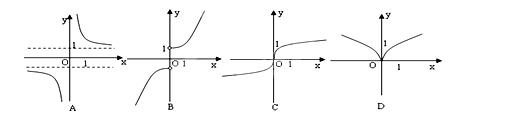
A
解析试题分析:因为函数的定义域为 ,又
,又 ,所以函数
,所以函数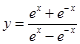 是奇函数,其图像关于原点对称,所以选项C、D排除。又
是奇函数,其图像关于原点对称,所以选项C、D排除。又 ,所以函数
,所以函数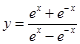 在
在 内单调递减,因此选项B排除,所以选A。
内单调递减,因此选项B排除,所以选A。
考点:函数的图像;函数的单调性;函数的奇偶性。
点评:我们通常利用函数的定义域、值域、单调性、奇偶性、特殊值(或特殊点)来判断函数的图像。本题就是根据函数的定义域排除C,根据奇偶性排除D,根据单调性排除B,从而选出正确答案。

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
若f(x)为R上的奇函数,给出下列四个说法:
①f(x)+f(-x)=0 ; ②f(x)-f(-x)=2f(x);
③f(x)·f(-x)<0; ④ 。其中一定正确的有( )
。其中一定正确的有( )
| A.0个 | B.1个 | C.2个 | D.3个 |
函数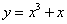 的递增区间是( )
的递增区间是( )
A.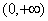 | B. | C.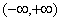 | D.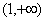 |
若函数f(x)=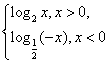 ,若f(a)>f(-a),则实数a的取值范围是( )
,若f(a)>f(-a),则实数a的取值范围是( )
| A.(-1,0)∪(0,1) | B.(-∞,-1)∪(1,+∞) |
| C.(-1,0)∪(1,+∞) | D.(-∞,-1)∪(0,1) |
函数 定义如下:对任意
定义如下:对任意 ,当
,当 为有理数时,
为有理数时, ;当
;当 为无理数时,
为无理数时, ;则称函数
;则称函数 为定义在实数上的狄利克雷拓展函数.下列关于函数
为定义在实数上的狄利克雷拓展函数.下列关于函数 说法错误的是( )
说法错误的是( )
A. 的值域为 的值域为 |
B. 是偶函数 是偶函数 |
C. 是周期函数且 是周期函数且 是 是 的一个周期 的一个周期 |
D. 在实数集上的任何区间都不是单调函数 在实数集上的任何区间都不是单调函数 |
函数 的一个单调递增区间是( )
的一个单调递增区间是( )
A. | B. | C. | D. |
已知函数f(x)=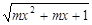 的定义域是一切实数,则m的取值范围是( )
的定义域是一切实数,则m的取值范围是( )
| A.0<m≤4 | B.0≤m≤1 | C.m≥4 | D.0≤m≤4 |
当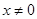 时,有不等式( )
时,有不等式( )
A.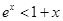 |
B.当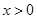 时 时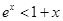 ,当 ,当 时 时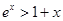 |
C.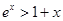 |
D.当 时 时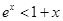 ,当 ,当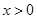 时 时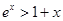 |
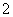 的等边三角形
的等边三角形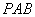 沿
沿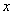 轴滚动,某时刻
轴滚动,某时刻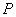 与坐标原点重合(如图),设顶点
与坐标原点重合(如图),设顶点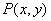 的轨迹方程是
的轨迹方程是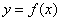 ,关于函数
,关于函数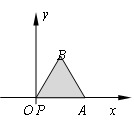
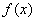 的值域为
的值域为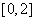 ;
;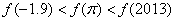 ;
;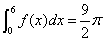 .
.