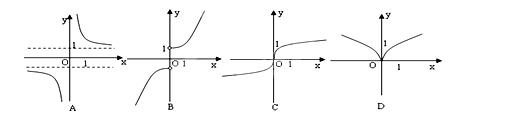
题目内容
若函数f(x)=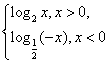 ,若f(a)>f(-a),则实数a的取值范围是( )
,若f(a)>f(-a),则实数a的取值范围是( )
| A.(-1,0)∪(0,1) | B.(-∞,-1)∪(1,+∞) |
| C.(-1,0)∪(1,+∞) | D.(-∞,-1)∪(0,1) |
C
解析试题分析:根据函数解析式可知,f(x)=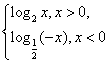 在定义域x<0,x>0上递增,且该函数为奇函数,那么可知f(a)>f(-a),等价f(a)>0,那么则有a>1,或者0<a<1,因此可知不等式的解集为(-1,0)∪(1,+∞),选C.
在定义域x<0,x>0上递增,且该函数为奇函数,那么可知f(a)>f(-a),等价f(a)>0,那么则有a>1,或者0<a<1,因此可知不等式的解集为(-1,0)∪(1,+∞),选C.
考点:对数函数的单调性
点评:本题主要考查函数的对数的单调性、对数的基本运算及分类讨论思想,属于中等题。
由分段函数的表达式知,需要对a的正负进行分类讨论。

练习册系列答案
相关题目
设f(x)是定义在R上的偶函数,对x∈R,都有f(x+4)=f(x),且当x∈[-2,0]时,f(x)=( )x-1,若在区间(-2,6]内关于x的方程f(x)-loga(x+2)=0(a>1)恰有3个不同的实数根,则a的取值范围是
)x-1,若在区间(-2,6]内关于x的方程f(x)-loga(x+2)=0(a>1)恰有3个不同的实数根,则a的取值范围是
| A.(1,2) | B.(2,+∞) | C.(1, ) ) | D.( ,2) ,2) |
下列函数中,在其定义域内既是奇函数又是减函数的是( )
A. | B.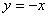 | C.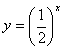 | D.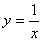 |
函数 的零点个数是
的零点个数是
| A.0 | B.1 |
| C.2 | D.3 |
为了得到函数 的图象,只需要把函数
的图象,只需要把函数 的图象上的所有点( )
的图象上的所有点( )
A.向右平行移动 个单位 个单位 | B.向右平行移动 个单位 个单位 |
C.向左平行移动 个单位 个单位 | D.向左平行移动 个单位 个单位 |
已知函数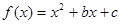 ,其中
,其中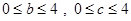 ,记函数
,记函数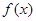 满足条件:
满足条件: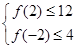 为事件
为事件 ,则事件
,则事件 发生的概率为( )
发生的概率为( )
A.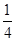 | B. | C.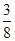 | D.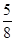 |
 的图象如图所示,则导函数
的图象如图所示,则导函数 的图象可能是 ( )
的图象可能是 ( )
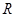 上的函数
上的函数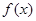 满足:
满足: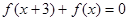 ,且函数
,且函数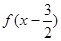 为奇函数。给出以下3个命题:
为奇函数。给出以下3个命题: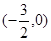 对称;
对称; 轴对称。
轴对称。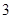
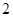


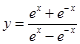 的图象大致为( ).
的图象大致为( ).