题目内容
【题目】已知函数![]() .
.
(1)若![]() ,求
,求![]() 的单调区间;
的单调区间;
(2)若关于![]() 的方程
的方程![]() 有四个不同的解
有四个不同的解![]() ,求实数
,求实数![]() 应满足的条件;
应满足的条件;
(3)在(2)条件下,若![]() 成等比数列,用
成等比数列,用![]() 表示t.
表示t.
【答案】(1)![]() 在
在![]() 单调递增,在
单调递增,在![]() 单调递减;(2)
单调递减;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)将![]() 代入,用分类讨论的去掉绝对值符号后结合函数单调性性质得解;
代入,用分类讨论的去掉绝对值符号后结合函数单调性性质得解;
(2)用分类讨论的去掉绝对值符号得分段函数,然后用导数研究函数的单调性,求出满足条件的![]() 的关系;
的关系;
(3)由韦达定理得![]() 两两互为倒数,结合等比数列性质及韦达定理可用
两两互为倒数,结合等比数列性质及韦达定理可用![]() 表示出
表示出![]() .
.
(1)![]() 时,
时, ,
,
易知在![]() 时,
时,![]() 是增函数,
是增函数,![]() 是减函数,
是减函数,
所以![]() 的单调增区间
的单调增区间![]() ,单调减区间是
,单调减区间是![]() .
.
(2) ,
,
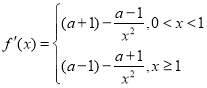 ,
,
当![]() 时,
时,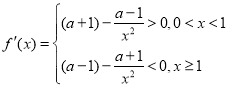
![]() 在
在![]() 是递增,在
是递增,在![]() 上递减,不合题意;
上递减,不合题意;
当![]() 时,
时, ![]() 时,由
时,由![]() 得
得![]() ,
,![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 是单调递增,
是单调递增,
![]() 时,由
时,由![]() 得
得![]() ,
,![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 是单调递增,
是单调递增,
又![]() ,
,![]() ,
,
∴实数![]() 应满足的条件是
应满足的条件是![]() .
.
(3)![]() ,即
,即![]() 或
或![]() ,
,
即![]() 或
或![]() ,
,
在![]() 中用
中用![]() 代换
代换![]() 得
得![]() ,即
,即![]() ,
,
∴方程![]() 与方程
与方程![]() 的根互为倒数.
的根互为倒数.
设这四个根从小到大依次为![]() ,则
,则![]() ,
,
所以![]() ,
,
若![]() 成等比数列,则
成等比数列,则![]() ,
,![]() ,
,![]() ,
,![]() .
.
∴![]() ,
,![]() ,
,
![]() ,
,
∴![]() ,
,
∴![]() .
.

 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案【题目】王先生购买了一部手机,欲使用中国移动“神州行”卡或加入联通的![]() 网,经调查其收费标准见下表:(注:本地电话费以分为计费单位,长途话费以秒为计费单位.)
网,经调查其收费标准见下表:(注:本地电话费以分为计费单位,长途话费以秒为计费单位.)
网络 | 月租费 | 本地话费 | 长途话费 |
甲:联通 |
|
|
|
乙:移动“神州行” | 无 |
|
|
若王先生每月拨打本地电话的时间是拨打长途电话时间的![]() 倍,若要用联通
倍,若要用联通![]() 应最少打多长时间的长途电话才合算.( )
应最少打多长时间的长途电话才合算.( )
A.![]() 秒B.
秒B.![]() 秒C.
秒C.![]() 秒D.
秒D.![]() 秒
秒
【题目】高铁、移动支付、网购与共享单车被称为中国的新四大发明,为了解永安共享单车在淮南市的使用情况,永安公司调查了100辆共享单车每天使用时间的情况,得到了如图所示的频率分布直方图.
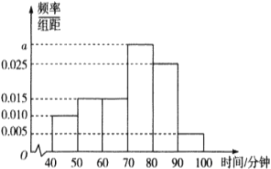
(Ⅰ)求图中![]() 的值;
的值;
(Ⅱ)现在用分层抽样的方法从前3组中随机抽取8辆永安共享单车,将该样本看成一个总体,从中随机抽取2辆,求其中恰有1辆的使用时间不低于50分钟的概率;
(Ⅲ)为进一步了解淮南市对永安共享单车的使用情况,永安公司随机抽取了200人进行调查问卷分析,得到如下2×2列联表:
经常使用 | 偶尔使用或不用 | 合计 | |
男性 | 50 | 100 | |
女性 | 40 | ||
合计 | 200 |
完成上述2×2列联表,并根据表中的数据判断是否有85%的把握认为淮南市使用永安共享单车的情况与性别有关?
附: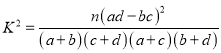
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |