题目内容
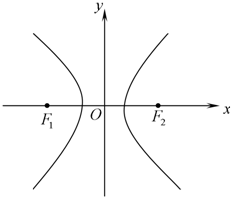
已知点F1,F2是双曲线M: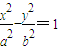 的左右焦点,其渐近线为
的左右焦点,其渐近线为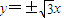 ,且右顶点到左焦点的距离为3.
,且右顶点到左焦点的距离为3.(1)求双曲线M的方程;
(2)过F2的直线l与M相交于A、B两点,直线l的法向量为
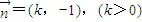 ,且
,且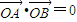 ,求k的值;
,求k的值;(3)在(2)的条件下,若双曲线M在第四象限的部分存在一点C满足
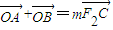 ,求m的值及△ABC的面积S△ABC.
,求m的值及△ABC的面积S△ABC.
【答案】分析:(1)由渐近线为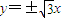 ,且右顶点到左焦点的距离为3,得到a=1,b=
,且右顶点到左焦点的距离为3,得到a=1,b=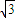 ,c=2,由此能求出双曲线方程.
,c=2,由此能求出双曲线方程.
(2)直线l的方程为y=k(x-2),由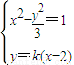 得(3-k2)x2+4k2x-(4k2+3)=0,再由韦达定理和平面向量知识能够得到k.
得(3-k2)x2+4k2x-(4k2+3)=0,再由韦达定理和平面向量知识能够得到k.
(3)把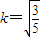 代入(3-k2)x2+4k2x-(4k2+3)=0,得4x2+4x-9=0,此时
代入(3-k2)x2+4k2x-(4k2+3)=0,得4x2+4x-9=0,此时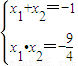 ,所以
,所以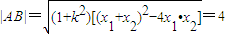 .由此入手能求出m的值及△ABC的面积S△ABC.
.由此入手能求出m的值及△ABC的面积S△ABC.
解答:解:(1)∵渐近线为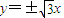 ,且右顶点到左焦点的距离为3.
,且右顶点到左焦点的距离为3.
∴a=1,b=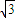 ,c=2,
,c=2,
∴双曲线方程为: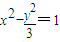 .…(4分)
.…(4分)
(2)直线l的方程为y=k(x-2),由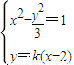 得(3-k2)x2+4k2x-(4k2+3)=0(*)
得(3-k2)x2+4k2x-(4k2+3)=0(*)
所以 …(6分)
…(6分)
由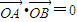 得x1•x2+y1•y2=0
得x1•x2+y1•y2=0
即(1+k2)x1•x2-2k2(x1+x2)+4k2=0
代入化简,并解得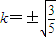 (舍去负值),
(舍去负值),
∴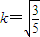 .…(9分)
.…(9分)
(3)把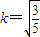 代入(*)并化简得4x2+4x-9=0,
代入(*)并化简得4x2+4x-9=0,
此时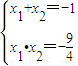 ,
,
所以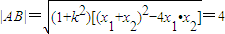 …(11分)
…(11分)
设C(x,y),由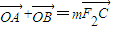 得
得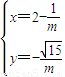 代入双曲线M的方程解得
代入双曲线M的方程解得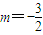 (舍),m=2,所以
(舍),m=2,所以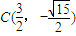 ,…(14分)
,…(14分)
点C到直线AB的距离为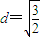 ,
,
所以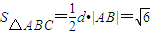 .…(16分)
.…(16分)
点评:本题主要考查双曲线标准方程,简单几何性质,直线与双曲线的位置关系,圆的简单性质等基础知识.考查运算求解能力,推理论证能力;考查函数与方程思想,化归与转化思想.
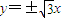 ,且右顶点到左焦点的距离为3,得到a=1,b=
,且右顶点到左焦点的距离为3,得到a=1,b=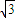 ,c=2,由此能求出双曲线方程.
,c=2,由此能求出双曲线方程.(2)直线l的方程为y=k(x-2),由
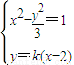 得(3-k2)x2+4k2x-(4k2+3)=0,再由韦达定理和平面向量知识能够得到k.
得(3-k2)x2+4k2x-(4k2+3)=0,再由韦达定理和平面向量知识能够得到k.(3)把
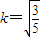 代入(3-k2)x2+4k2x-(4k2+3)=0,得4x2+4x-9=0,此时
代入(3-k2)x2+4k2x-(4k2+3)=0,得4x2+4x-9=0,此时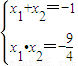 ,所以
,所以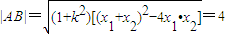 .由此入手能求出m的值及△ABC的面积S△ABC.
.由此入手能求出m的值及△ABC的面积S△ABC.解答:解:(1)∵渐近线为
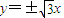 ,且右顶点到左焦点的距离为3.
,且右顶点到左焦点的距离为3.∴a=1,b=
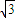 ,c=2,
,c=2,∴双曲线方程为:
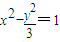 .…(4分)
.…(4分)(2)直线l的方程为y=k(x-2),由
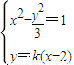 得(3-k2)x2+4k2x-(4k2+3)=0(*)
得(3-k2)x2+4k2x-(4k2+3)=0(*)所以
 …(6分)
…(6分)由
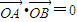 得x1•x2+y1•y2=0
得x1•x2+y1•y2=0即(1+k2)x1•x2-2k2(x1+x2)+4k2=0
代入化简,并解得
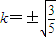 (舍去负值),
(舍去负值),∴
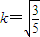 .…(9分)
.…(9分)(3)把
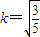 代入(*)并化简得4x2+4x-9=0,
代入(*)并化简得4x2+4x-9=0,此时
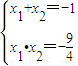 ,
,所以
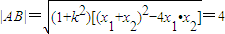 …(11分)
…(11分)设C(x,y),由
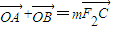 得
得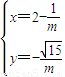 代入双曲线M的方程解得
代入双曲线M的方程解得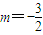 (舍),m=2,所以
(舍),m=2,所以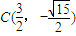 ,…(14分)
,…(14分)点C到直线AB的距离为
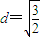 ,
,所以
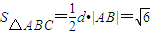 .…(16分)
.…(16分)点评:本题主要考查双曲线标准方程,简单几何性质,直线与双曲线的位置关系,圆的简单性质等基础知识.考查运算求解能力,推理论证能力;考查函数与方程思想,化归与转化思想.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
 的左、右两个焦点,点P是双曲线上一点,且|PF1|.|PF2|=32,求∠F1PF2的大小.
的左、右两个焦点,点P是双曲线上一点,且|PF1|.|PF2|=32,求∠F1PF2的大小.