题目内容
给出一列三个命题:
①函数f(x)=x|x|+bx+c为奇函数的充要条件是c=0;
②若函数f(x)=lg(x2+ax-a)的值域是R,则a≤-4,或a≥0;
③若函数y=f(x-1)是偶函数,则函数y=f(x)的图象关于直线x=0对称.
其中正确的命题序号是
①函数f(x)=x|x|+bx+c为奇函数的充要条件是c=0;
②若函数f(x)=lg(x2+ax-a)的值域是R,则a≤-4,或a≥0;
③若函数y=f(x-1)是偶函数,则函数y=f(x)的图象关于直线x=0对称.
其中正确的命题序号是
①②
①②
.分析:①当c=0时,f(x)=x|x|+bx,用定义可以验证其为奇函数,反之,若函数为奇函数,由f(-x)=-f(x)恒成立可以得到c=0;②函数值域为R,说明y=x2+ax-a能取遍所有正实数,故△≥0,可解得a的范围;③根据图象变换可知函数f(x)的图象关于直线x=-1对称.
解答:解:①当c=0时,f(x)=x|x|+bx
∵f(-x)=(-x)|-x|+b(-x)=-x|x|-bx=-(x|x|+bx)=-f(x)
∴函数f(x)为奇函数.
反之,∵函数f(x)=x|x|+bx+c为奇函数
∴f(-x)=-f(x)恒成立
∴-x|-x|+b(-x)+c=-x|x|-bx-c恒成立
∴2c=0
即c=0
∴函数f(x)=x|x|+bx+c为奇函数的充要条件是c=0.
②∵函数f(x)=lg(x2+ax-a)的值域是R,
∴函数y=x2+ax-a能取遍一切正实数.
∴△=a2-4×(-a)=a2+4a≥0
解得a≤-4,或a≥0.
③∵函数函数y=f(x-1)的图象是偶函数,
∴函数图象关于y轴对称,
∵函数y=f(x)的图象可以由函数y=f(x-1)的图象向左平移一个单位得到
故函数y=f(x)的图象关于直线x=-1对称.
故正确的是①②
∵f(-x)=(-x)|-x|+b(-x)=-x|x|-bx=-(x|x|+bx)=-f(x)
∴函数f(x)为奇函数.
反之,∵函数f(x)=x|x|+bx+c为奇函数
∴f(-x)=-f(x)恒成立
∴-x|-x|+b(-x)+c=-x|x|-bx-c恒成立
∴2c=0
即c=0
∴函数f(x)=x|x|+bx+c为奇函数的充要条件是c=0.
②∵函数f(x)=lg(x2+ax-a)的值域是R,
∴函数y=x2+ax-a能取遍一切正实数.
∴△=a2-4×(-a)=a2+4a≥0
解得a≤-4,或a≥0.
③∵函数函数y=f(x-1)的图象是偶函数,
∴函数图象关于y轴对称,
∵函数y=f(x)的图象可以由函数y=f(x-1)的图象向左平移一个单位得到
故函数y=f(x)的图象关于直线x=-1对称.
故正确的是①②
点评:本题主要考查了函数的性质及函数的图象、充要条件的判断,尤其第二个命题容易判断为△<0而产生错误.

练习册系列答案
相关题目
 ,从中选取若干项,不改变它们在原来数列中的先后次序,得到的数列称为是原来数列的一个子数列. 某同学在学习了这一个概念之后,打算研究首项为
,从中选取若干项,不改变它们在原来数列中的先后次序,得到的数列称为是原来数列的一个子数列. 某同学在学习了这一个概念之后,打算研究首项为 ,公差为
,公差为 的无穷等差数列
的无穷等差数列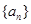 的子数列问题,为此,他取了其中第一项
的子数列问题,为此,他取了其中第一项 ,第三项
,第三项 和第五项
和第五项 .
. 成等比数列,求
成等比数列,求 ,
,  的无穷等差数列
的无穷等差数列 ,使得数列
,使得数列 ,公比为正整数
,公比为正整数 (
( )的无穷等比数 列
)的无穷等比数 列 ,总可以找到一个子数列
,总可以找到一个子数列 ,使得
,使得 ,由
,由 与
与 的大小关系去判断该命题是否正确. 他将得到什么结论?
的大小关系去判断该命题是否正确. 他将得到什么结论?