题目内容
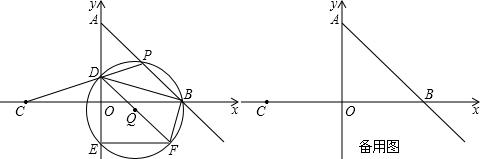
如图,四边形ABCD内接于圆O,∠BOD=110°,∠BCD等于( )


| A、100° | B、110° | C、125° | D、135° |
考点:圆內接多边形的性质与判定,弦切角
专题:计算题,几何证明
分析:利用同弧所对的圆周角与圆心角的关系,易求得圆周角∠BAD的度数;由于圆内接四边形的内对角互补,则∠BAD+∠BCD=180°,由此可求得∠BCD的度数.
解答:解:∵四边形ABCD内接于⊙O,
∴∠BAD+∠BCD=180°,
∵∠BAD=
∠BOD=55°,
∴∠BCD=180°-∠BAD=125°;
故选:C.
∴∠BAD+∠BCD=180°,
∵∠BAD=
| 1 |
| 2 |
∴∠BCD=180°-∠BAD=125°;
故选:C.
点评:此题主要考查的是圆内接四边形的性质及圆周角定理的综合应用能力.

练习册系列答案
相关题目
某高校《统计》课程的教师随机给出了选该课程的一些情况,具体数据如下:
为了判断选修统计专业是否与性别有关,根据表中数据,得K2≈4.844,所以可以判定选修统计专业与性别有关.那么这种判断出错的可能性为( )
| 非统计专业 | 统计专业 | |
| 男 | 13 | 10 |
| 女 | 7 | 20 |
| A、5% | B、95% |
| C、1% | D、99% |
若函数f(x)=|x+2|+|x-3|的最小值为n,则二项式(x2+
)n的展开式中的常数项是( )
| 2 | ||
|
| A、第3项 | B、第4项 |
| C、第5项 | D、第6项 |
在极坐标系中,曲线C:p=2cosθ上任意一点P到点Q(
,
)的最大距离等于( )
| 2 |
| π |
| 4 |
A、
| ||
| B、2 | ||
C、
| ||
D、
|
-1+2i是下列哪个实系数方程的一个根( )
| A、x2-4x+5=0 | B、x2+4x+5=0 | C、x2-2x+5=0 | D、x2+2x+5=0 |
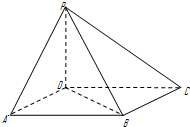 如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2AD=2,PD⊥底面ABCD,且PD=AD,求:平面PAB的一个法向量.
如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2AD=2,PD⊥底面ABCD,且PD=AD,求:平面PAB的一个法向量.