Question

【题目】已知函数，下列命题：

①的定义域为；

②是奇函数；

③在上单调递增；

④若实数满足，则；

⑤设函数在上的最大值为，最小值为，则.

其中真命题的序号是______.（写出所有真命题的序号）

Answer 1

【答案】①②③④．

【解析】

由对数的真数大于0，解不等式可判断①；由奇函数的定义，可判断②；由复合函数的单调性可判断③；由函数的奇偶性和单调性，解方程可判断④；由奇函数的性质：在对称区间上的最值之和为0，可判断⑤．

对于①，函数，由，得，当时，成立，当时，两边平方得成立．所以的定义域为，故①正确；

对于②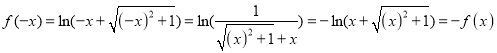，，所以是奇函数，故②正确；

对于③，令，设，

，

所以，所以在上单调递增，又在上单调递增，所以在上单调递增，又因为是奇函数，所以在上单调递增，故③正确；

对于④，若实数满足，则有所以，即有，故④正确；

对于⑤，为奇函数，，，∴，∴，故⑤不正确．

故答案为：①②③④．