题目内容
(2007
武汉模拟)已知点
在曲线
上，且
．
(1)
求f(x)的定义域；(2)
求证：
；
(3)
求证：数列
前n项和
，
答案：略
解析：
解析：
|
解析： (1)由 知x满足 ，
∴ ，∴ ，
∴  ，∴ ，
故 x＞0或x≤－1．f(x) 定义域为：
(2) ∵ ，则
于是有：  ．
要证明  ，
只需证明：  ．(*)
下面使用数学归纳法证明：  ．
①在 n=1时， ， ，则n=1时(*)式成立．
②假设 n=k时， 成立，
由  ，
要证明：  ，
只需  ，
只需  ，
只需  ．
而  在 时恒成立．于是 ．
于是  ．
又  ，
要证：  ，
只需证：  ，
只需证：  ，而 在k≥1时恒成立．
于是：  ．
因此  得证．
综合①②可知 (*)式得证．从而原不等式成立．(3) 要证明： ，由(2)可知只需证： ．(**)
下面分析证明：（ **）式成立．要使 (**)成立，只需证： ，
即只需证：
而 2n＞1在n 1时显然成立．故(**)式得证．
于是由 (**)式可知有： ，
因此有：  ． |
练习册系列答案
相关题目
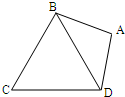（2007•武汉模拟）如图，在平面四边形ABCD中，AB=AD=1，∠BAD=θ，而△BCD是正三角形，
（2007•武汉模拟）如图，直线l：y=