Question

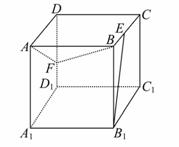
如图，正方体ABCD－A₁B₁C₁D₁的棱长为1，E、F分别是棱BC、DD₁上的点，如果B₁E⊥平面ABF，则CE与DF的长度之和为　　　　.

Answer 1

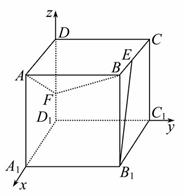以D₁为坐标原点，D₁A₁、D₁C₁、D₁D所在直线分别为x，y，z轴建立空间直角坐标系D₁xyz，设CE＝a，DF＝b，

则易知E(a,1,1)，B₁(1,1,0)⇒＝(a－1,0,1)，

又F(0,0,1－b)，B(1,1,1)⇒＝(1,1，b)，

由于AB⊥B₁E，

故若B₁E⊥平面ABF，

只需·＝(1,1，b)·(a－1,0,1)＝0⇒a＋b＝1.

答案：1