题目内容
选修4—4：坐标系与参数方程
已知椭圆
C的极坐标方程为
，点
为其左、右焦点，直线
的参数方程为
（
为参数，
）．求点到直线
的距离之和.
【解析】
试题分析：首先将椭圆的极坐标转化为直角坐标利用：
，进而找到椭圆的两个焦点坐标，同时将直线方程也化为普通方程，利用点到直线的距离公式，分别求得两个焦点到直线
的距离，进而求得距离和.
试题解析：直线
普通方程为
；曲线
的普通方程为
．
∵
,
，∴点
到直线
的距离
点
到直线的距离
∴
.
考点：1.极坐标方程；2.直线的参数方程；3.点到直线的距离公式.
练习册系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
为 
（其中
），其部分图像如下图所示，将
的图像纵坐标不变，横坐标变成原来的2倍，再向右平移1个单位得到
的图像，则函数
B.
D.
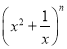的二项展开式的各项系数和为32，则二项展开式中含
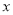项的系数为________.
B. 
C. 
D. 
分，未中扣
分，每位同学原始积分均为
分，当累积得分少于或等于
分则停止投篮，否则继续，每位同学最多投篮
次.且规定总共投中
次的同学分别为一、二、三等奖，奖金分别为
元、
元、
元.某班甲、乙、丙同学相约参加此活动，他们每次投篮命中的概率均为
，且互不影响.
，求
.
在椭圆
上,
为椭圆
的右焦点,若点
满足
且
,则
的最小值为( )
B．3 C．
D． 1
则xy的取值范围是 ．