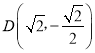题目内容
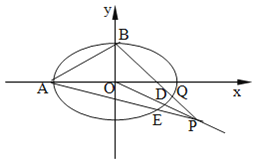
【题目】已知圆![]() :
:![]() ,过坐标原点
,过坐标原点![]() 的直线
的直线![]() 交
交![]() 于
于![]() ,
,![]() 两点,点
两点,点![]() 在第一象限,
在第一象限,![]() 轴,垂足为
轴,垂足为![]() .连结
.连结![]() 并延长交
并延长交![]() 于点
于点![]() .
.
(1)设![]() 到直线
到直线![]() 的距离为
的距离为![]() ,求
,求![]() 的取值范围;
的取值范围;
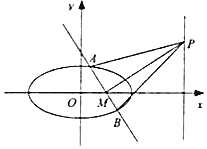
(2)求![]() 面积的最大值及此时直线
面积的最大值及此时直线![]() 的方程.
的方程.
【答案】(1)![]()
(2)![]() 的最大值为
的最大值为![]() ,直线
,直线![]() :
:![]()
【解析】
(1)设直线![]() 的方程为
的方程为![]() ,与圆的方程联立,构成方程组,解出
,与圆的方程联立,构成方程组,解出![]() ,
,![]() 的坐标,再利用点线的距离公式求解;
的坐标,再利用点线的距离公式求解;
(2)把直线![]() 的方程与圆的方程联立,得到关于
的方程与圆的方程联立,得到关于![]() 的一元二次方程,运用根与系数的关系可求得点
的一元二次方程,运用根与系数的关系可求得点![]() 的横坐标,进而表示出
的横坐标,进而表示出![]() 的面积,再通过化简变形,结合双勾函数的性质求得最大值及相应的直线方程.
的面积,再通过化简变形,结合双勾函数的性质求得最大值及相应的直线方程.
(1) 设直线![]() 的方程为
的方程为![]() ,
,
与圆的方程联立有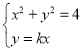 ,
,
消![]() 并整理得,
并整理得,![]() ,
,
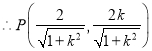 ,
,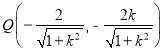 ,
,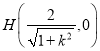 ,
,
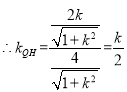 ,
,
![]() 直线
直线![]() 的方程为
的方程为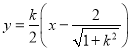 ,
,
即![]() ,
,
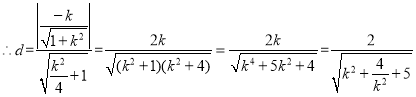 ,
,
![]() ,
,
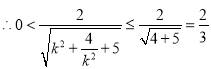 ,即
,即![]() ;
;
(2) 直线![]() 与圆的方程联立有,
与圆的方程联立有,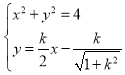 ,
,
消![]() 并整理得,
并整理得,![]() ,
,
由根与系数的关系有,![]() ,
,
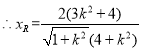 ,
,
![]()
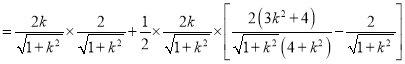
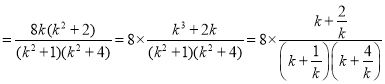
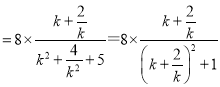 ,
,
令![]() ,则
,则![]() ,当且仅当
,当且仅当![]() 时取等号,
时取等号,
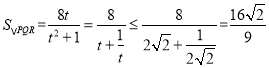 ,
,
故![]() 面积的最大值为
面积的最大值为![]() ,直线
,直线![]() :
:![]() .
.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目