题目内容
如图2-3-11,过S引三条长度相等但不共面的线段SA、SB、SC,且∠ASB=∠ASC=60°,∠BSC=90°.
图2-3-11
求证:平面ABC⊥平面BSC.
思路分析:它可以用两种方法来证明,一是作平面的垂线而后证明它在另一个平面内(证法一);二是在一个平面内找一条线段,证明它与另一个平面垂直(证法二).
证明一:作AD⊥平面BSC,D为垂足.
∵∠ASB=∠ASC=60°,SA=SB=SC,则AS=AB=AC,
∴D为△BSC的外心.又∠BSC=90°,
∴D为BC的中点,即AD在平面ABC内.
∴平面ABC⊥平面BSC.
证明二:取BC的中点D,连结AD、SD,易证AD⊥BC.
又△ABS是正三角形,△BSC为等腰直角三角形,
∴BD=SD.
∴AD2+SD2=AD2+BD2=AB2=AS2.
由勾股定理的逆定理,知AD⊥SD,
∴AD⊥平面BSC.
又AD![]() 平面ABC,∴平面ABC⊥平面BSC.
平面ABC,∴平面ABC⊥平面BSC.
绿色通道:证明面面垂直的关键是将“面面垂直”的问题转化为证明“线面垂直”的问题,将线面垂直问题再进一步转化为“线线垂直”问题去解决.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (2012•宝鸡模拟)(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分)
(2012•宝鸡模拟)(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分)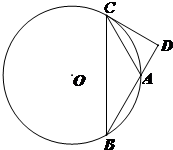 (2013•朝阳区一模)如图,圆O是△ABC的外接圆,过点C作圆O的切线交BA的延长线于点D.若
(2013•朝阳区一模)如图,圆O是△ABC的外接圆,过点C作圆O的切线交BA的延长线于点D.若
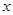 轴上是否存在一点H,使D、G、F、H四点围成的四边形周长最小.若存在,求出这个最小值及G、H的坐标;若不存在,请说明理由.
轴上是否存在一点H,使D、G、F、H四点围成的四边形周长最小.若存在,求出这个最小值及G、H的坐标;若不存在,请说明理由.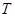 ,过点
,过点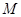 ,过点
,过点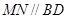 ,交线段
,交线段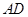 于点
于点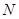 ,连接
,连接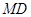 ,使
,使 ~
~ ,若存在,求出点
,若存在,求出点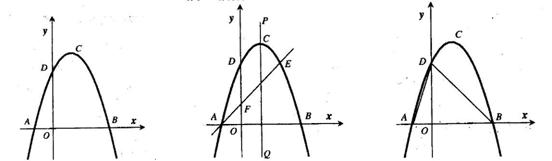 图1
图2
图3
图1
图2
图3