题目内容
(本题满分12分)
已知点P(-1,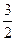 )是椭圆E:
)是椭圆E: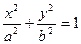 (
(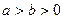 )上一点,F1、F2分别是椭圆E的左、右焦点,O是坐标原点,PF1⊥x轴.
)上一点,F1、F2分别是椭圆E的左、右焦点,O是坐标原点,PF1⊥x轴.
(1)求椭圆E的方程;
(2)设A、B是椭圆E上两个动点,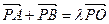 (0<λ<4,且λ≠2).求证:直线AB的斜率等于椭圆E的离心率;
(0<λ<4,且λ≠2).求证:直线AB的斜率等于椭圆E的离心率;
(3)在(2)的条件下,当△PAB面积取得最大值时,求λ的值.
已知点P(-1,
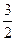 )是椭圆E:
)是椭圆E: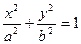 (
(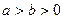 )上一点,F1、F2分别是椭圆E的左、右焦点,O是坐标原点,PF1⊥x轴.
)上一点,F1、F2分别是椭圆E的左、右焦点,O是坐标原点,PF1⊥x轴.(1)求椭圆E的方程;
(2)设A、B是椭圆E上两个动点,
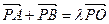 (0<λ<4,且λ≠2).求证:直线AB的斜率等于椭圆E的离心率;
(0<λ<4,且λ≠2).求证:直线AB的斜率等于椭圆E的离心率;(3)在(2)的条件下,当△PAB面积取得最大值时,求λ的值.
解:(1)∵PF1⊥ x轴,
x轴,
∴F1(-1,0),c=1,F2(1,0),
|PF2|=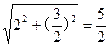 ,2a=|PF1|+|PF2|=4,a=2,b2=3,
,2a=|PF1|+|PF2|=4,a=2,b2=3,
椭圆E的方程为: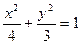 ;…………………3分
;…………………3分
⑶设直线AB的方程为y=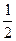 x+t,
x+t,
与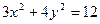 联立消去y并整理得 x2+tx+t2-3=0,
联立消去y并整理得 x2+tx+t2-3=0,
△=3(4-t2),
AB|=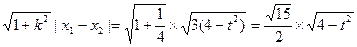 ,
,
点P到直线AB的距离为d=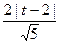 ,
,
△ PAB的面 积为S
积为S =
=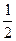 |AB|×d=
|AB|×d=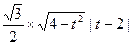 , ………10分
, ………10分
设f(t)=S2=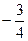 (t4-4t3+16t-16) (-2<t<2),
(t4-4t3+16t-16) (-2<t<2),
f’(t)=-3(t3-3t2+4)=-3(t+1)(t-2)2,由f’(t)=0及-2<t<2得t=-1.
当t∈(-2,-1)时,f’(t)>0,当t∈(-1,2)时,f’(t)<0,f(t)=-1时取得最大值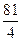 ,
,
所以S的最大值为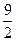 .
.
此时x1+x2=-t=1=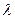 -2,
-2,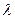 =3.……………………………………12分
=3.……………………………………12分
 x轴,
x轴,∴F1(-1,0),c=1,F2(1,0),
|PF2|=
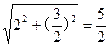 ,2a=|PF1|+|PF2|=4,a=2,b2=3,
,2a=|PF1|+|PF2|=4,a=2,b2=3,椭圆E的方程为:
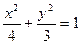 ;…………………3分
;…………………3分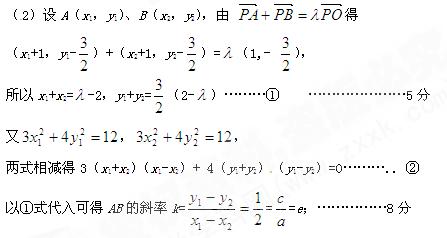
⑶设直线AB的方程为y=
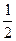 x+t,
x+t,与
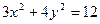 联立消去y并整理得 x2+tx+t2-3=0,
联立消去y并整理得 x2+tx+t2-3=0,△=3(4-t2),
AB|=
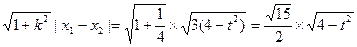 ,
,点P到直线AB的距离为d=
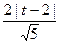 ,
,△ PAB的面
 积为S
积为S =
=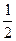 |AB|×d=
|AB|×d=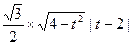 , ………10分
, ………10分设f(t)=S2=
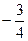 (t4-4t3+16t-16) (-2<t<2),
(t4-4t3+16t-16) (-2<t<2),f’(t)=-3(t3-3t2+4)=-3(t+1)(t-2)2,由f’(t)=0及-2<t<2得t=-1.
当t∈(-2,-1)时,f’(t)>0,当t∈(-1,2)时,f’(t)<0,f(t)=-1时取得最大值
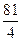 ,
,所以S的最大值为
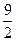 .
.此时x1+x2=-t=1=
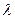 -2,
-2,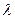 =3.……………………………………12分
=3.……………………………………12分略

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
 满分12
满分12 分)
分)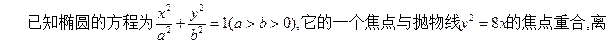
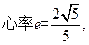 过椭圆的右焦点F作与坐标轴不垂直的直线l交椭圆于A、B两点.
过椭圆的右焦点F作与坐标轴不垂直的直线l交椭圆于A、B两点. 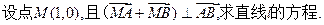
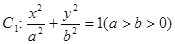 的左准线为
的左准线为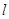 ,左右焦点分别为
,左右焦点分别为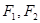 ,抛物线
,抛物线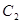 的准线为
的准线为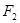 ,曲线
,曲线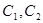 的一个交点为P,则
的一个交点为P,则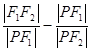 等于()
等于()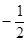 D
D 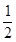
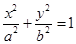
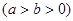 的离心率为
的离心率为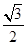 ,过右焦点
,过右焦点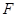 且斜率为
且斜率为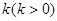 的直线与椭圆C相交于
的直线与椭圆C相交于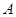 、
、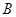 两点.若
两点.若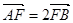 ,则
,则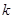 =( )
=( ) 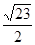
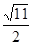
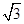
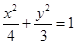 的中心和左焦点,点P为椭圆上的任意一点,则
的中心和左焦点,点P为椭圆上的任意一点,则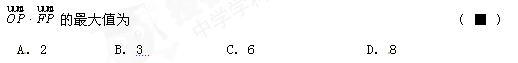
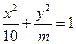 与双曲线
与双曲线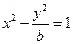 有相同的焦点,且椭圆与双曲线交于
有相同的焦点,且椭圆与双曲线交于 点
点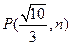 ,求椭圆及双曲线的方程.
,求椭圆及双曲线的方程.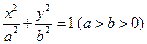 的
的 左焦点为F,右顶点为A,点B在椭圆上,且BF⊥x轴, 直线AB交
左焦点为F,右顶点为A,点B在椭圆上,且BF⊥x轴, 直线AB交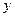 轴于点P,若
轴于点P,若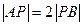 ,则椭圆的离心率是( )
,则椭圆的离心率是( )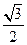

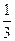
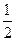
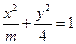 的焦距为2,则m的值等于
的焦距为2,则m的值等于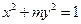 的离心率为
的离心率为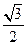 ,则它的长半轴长为_______________
,则它的长半轴长为_______________