题目内容

ABC的面积S满足≤S≤3，且=6，AB与BC的夹角为θ．
（1）求θ的取值范围．
（2）求函数f（θ）=sin2θ+2sinθcosθ+3cos2θ的最小值．

解：
（1）由题意知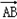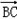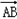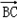：=||||cosθ=6，①
S=||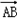||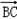sin（π﹣θ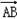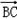）=||||sinθ，②
②÷①得=tanθ，即3tanθ=S．
由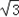≤S≤3，得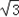≤3tanθ≤3，即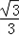≤tanθ≤1．
又θ为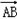与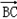的夹角，∴θ∈[0，π]，∴θ∈[，]．
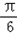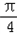（2）f（θ）=sin2θ+2sinθcosθ+3cos2θ=1+sin2θ+2cos2θ=2+sin2θ+cos2θ=2+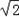sin（2θ+）
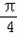∵θ∈[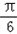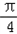，]，∴2θ+∈[，]．
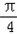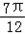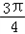∴当2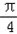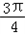θ+=，θ=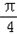时，f（θ）取最小值3．

练习册系列答案
相关题目
已知△ABC的面积S满足
3
≤S≤3
3
，且
AB
•
BC
=6．
（1）求角B的取值范围；
（2）求函数f(B)=
1-
2
cos(2B-
π
4
)
sinB
的值域．
已知△ABC的面积S满足3≤S≤3
3
，且
AB
•
BC
=6，
AB
与
BC
的夹角为α．
（1）求α的取值范围；
（2）若函数f（α）=sin2α+2sinαcosα+3cos2α，求f（α）的最小值，并指出取得最小值时的α．
已知△ABC的面积S满足
3
2
≤S≤
3
2
，且
AB
•
BC
=3，
AB
与
BC
的夹角为θ．
（1）求θ的取值范围；
（2）求函数f(θ)=3sin2θ+2
3
sinθ•cosθ+cos2θ的最大值及最小值．
在△ABC中，a、b、c分别为角A、B、C的对边，△ABC的面积S满足S=
3
2
bccosA．
（1）求角A的值；
（2）若a=
3
，设角B的大小为x，用x表示边c，并求c的最大值．
已知△ABC的面积S满足4≤S≤4
3
，且
AB
•
AC
=-8．
（Ⅰ）求角A的取值范围；
（Ⅱ）若函数f(x)=cos2
x
4
-2sin2
x
4
+3
3
sin
x
4
•cos
x
4
，求f（A）的最大值．