题目内容
已知a、b为单位向量，其夹角为60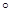
，则（2a－b）·b =( )
| A．－1 | B．0 | C．1 | D．2 |
B
解析试题分析：
=2×1×1×cos
-1=0，故选B.
【考点】向量的数量积运算.
练习册系列答案
全优点练单元计划系列答案
相关题目
，
，其中
为坐标原点.
且
，求向量
与
的夹角；
对任意实数
都成立，求实数
的取值范围.已知
均为单位向量，它们的夹角为
，那么
（ ）.
A． | B． | C． | D． |
已知向量
点P在
轴上，且使
有最小值，则点P 的坐标为
| A．（-3,0） | B．(2,0) | C．(3,0) | D．(4,0) |
已知向量
，若2
-
与垂直，则
（ ）.
A． | B． | C． | D．4 |
已知向量
，
，则以
，
为邻边的平行四边形的面积为( )
A． | B． | C．4 | D．8 |
若向量
满足：
则
| A．2 | B． | C．1 | D． |
如图,在平面四边形
中,
,
．若
,
,则
（）
A． | B． | C． | D． |
角
顶点在坐标原点O，始边
轴的非负半轴重合，点P在的终边上，点
，且
夹角的余弦值为（ ）
A． | B． | C． | D． |