题目内容
如图,在四棱锥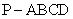 中,侧棱
中,侧棱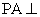 底面
底面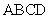 ,
,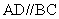 ,
,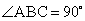 ,
,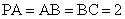 ,
,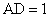 ,
,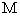 是棱
是棱 中点.
中点.
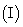 求证:
求证: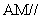 平面
平面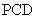 ;
;
 设点
设点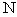 是线段
是线段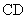 上一动点,且
上一动点,且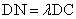 ,当直线
,当直线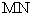 与平面
与平面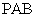 所成的角最大时,求
所成的角最大时,求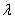 的值.
的值.
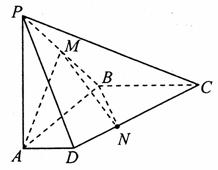
解:(1)以点A为原点建立如图所示的空间直角坐标系,则
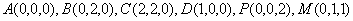
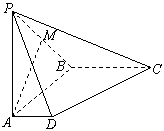 则
则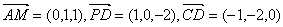
设平面PCD的法向量是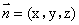 ,则
,则
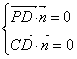 即
即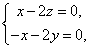
令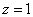 ,则
,则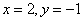 ,于是
,于是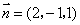
∵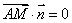 ,∴
,∴ ,
,
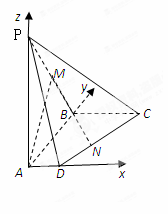 ∴AM//平面PCD ……6分
∴AM//平面PCD ……6分
(2)因为点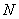 是线段
是线段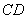 上的一点,可设
上的一点,可设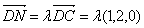
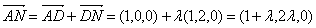
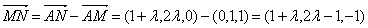
又面PAB的法向量为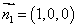
设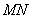 与平面
与平面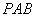 所成的角为
所成的角为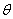
则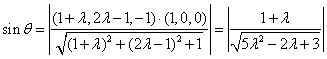
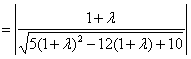
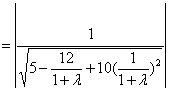
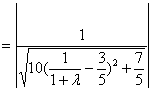
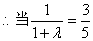 时, 即
时, 即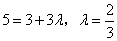 时,
时,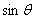 最大,
最大,
所以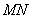 与平面
与平面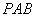 所成的角最大时
所成的角最大时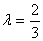 ……13分
……13分

练习册系列答案
相关题目
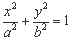 的左、右焦点,过F1且垂直于x轴的直线与椭圆交于A、B两点,若△ABF2为正三角形,则该椭圆的离心率
的左、右焦点,过F1且垂直于x轴的直线与椭圆交于A、B两点,若△ABF2为正三角形,则该椭圆的离心率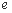 为 ( )
为 ( )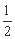 (B)
(B) 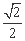 (C)
(C)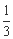 (D)
(D)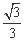
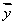 =0.15x+0.2。由回归直线方程可知,家庭年收入每增加1万元,,年教育支出平均增加 万元.
=0.15x+0.2。由回归直线方程可知,家庭年收入每增加1万元,,年教育支出平均增加 万元.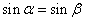 ,则
,则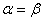 ”是真命题
”是真命题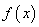 可导,且在
可导,且在 处有极值,则
处有极值,则
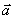 ,
, 的夹角为钝角的充要条件是
的夹角为钝角的充要条件是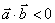
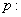 “
“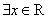 ,
,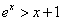 ”的否定是“
”的否定是“ ,
,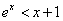 ”
” 中,内角
中,内角 ,
,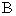 ,
,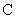 的对边分别为
的对边分别为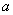 ,
,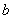 ,
,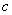 ,且满足
,且满足 ,则
,则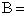 .
.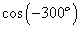 的值为( )
的值为( )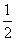 B.
B. C.-
C.- ,则
,则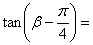 ( )[来
( )[来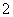 B.
B. C.
C. 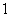 D.
D. 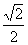
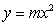 的准线距离为2,则
的准线距离为2,则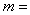 ( )
( ) 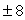 C.
C. 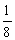 D.
D. 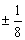
 题是( )
题是( )  , 则z是实数 B.若
, 则z是实数 B.若 , 则z是虚数
, 则z是虚数 数, 则
数, 则