题目内容
记函数f(x)=
的定义域为A,集合B=(2a,a+1)(a<1)
(1)求A
(2)若B⊆A,求实数a的取值范围.
| (x+1)•(x-1) |
(1)求A
(2)若B⊆A,求实数a的取值范围.
分析:(1)利用偶次根式的被开方数非负列不等式是解决本题的关键;准确求解一元二次不等式是解决本题的前提.
(2)由B⊆A得到集合B是集合A的子集,即集合B包含在集合A中,即可求出a的取值范围.
(2)由B⊆A得到集合B是集合A的子集,即集合B包含在集合A中,即可求出a的取值范围.
解答:解:(1)由题意得:(x+1)•(x-1)≥0
即A=(-∞,-1]∪[1,+∞)(4分)
(2)∵B⊆A,
∴2a≥1或a+1≤-1,
即a≥
或a≤-2(11分)
而a<1,
∴
≤a<1或a≤-2,(13分)
故当B⊆A时,实数a的取值范围是(-∞,-2]∪[
,1)(14分)
即A=(-∞,-1]∪[1,+∞)(4分)
(2)∵B⊆A,
∴2a≥1或a+1≤-1,
即a≥
| 1 |
| 2 |
而a<1,
∴
| 1 |
| 2 |
故当B⊆A时,实数a的取值范围是(-∞,-2]∪[
| 1 |
| 2 |
点评:本小题主要考查了函数定义域的求解,不等式的基本解法,集合交并运算的求解.考查学生等价转化的思想、数形结合的思想.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
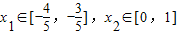 ,试求a的取值范围;
,试求a的取值范围;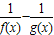 对任意x1,x2∈[1,3]恒有|H(x1)-H(x2)|≤a成立,试求a的取值范围.(参考:ln2≈0.7)
对任意x1,x2∈[1,3]恒有|H(x1)-H(x2)|≤a成立,试求a的取值范围.(参考:ln2≈0.7)