题目内容

已知点M是棱长为a的正方体ABCD-A1B1C1D1的棱DD1的中点，则过A，B，M三点的截面积是
5
4
a2
5
4
a2
．
分析：AM=
a2+
1
4
a2
=
5
2
a，BM=
2a2+
1
4
a2
=
3
2
a，AB=a，由余弦定理，得cos∠AMB=
5
4
a2+
9
4
a2-a2
2×
5
a
2
×
3a
2
=
5
3
，sin∠AMB=
1-(
5
3
)2
=
2
3
，由此能求出过A，B，M三点的截面积．
解答：解：AM=
a2+
1
4
a2
=
5
2
a，
BM=
2a2+
1
4
a2
=
3
2
a，
AB=a，
由余弦定理，得cos∠AMB=
5
4
a2+
9
4
a2-a2
2×
5
a
2
×
3a
2
=
5
3
，
∴sin∠AMB=
1-(
5
3
)2
=
2
3
，
∴过A，B，M三点的截面积S=
1
2
×
5
a
2
×
3a
2
×
2
3
=
5
4
a2．
故答案为：
5
4
a2．
点评：本题考查棱柱中截面面积的求法，解题时要认真审题，仔细解答，要熟练掌握棱柱的结构特征．
练习册系列答案
相关题目
精英家教网已知四棱锥P-ABCD，底面ABCD是∠A=60°、边长为a的菱形，又PD⊥底ABCD，且PD=CD，点M、N分别是棱AD、PC的中点．
（1）证明：DN∥平面PMB；
（2）证明：平面PMB⊥平面PAD；
（3）求点A到平面PMB的距离．
已知正方形ABCD的边长为1，AC∩BD=O．将正方形ABCD沿对角线BD折起，使AC=1，得到三棱锥A-BCD，如图所示．
（Ⅰ）若点M是棱AB的中点，求证：OM∥平面ACD；
（Ⅱ）求证：AO⊥平面BCD；
（Ⅲ）求二面角A-BC-D的余弦值．
精英家教网
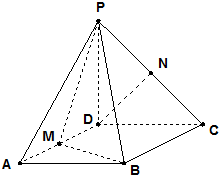已知四棱锥P-ABCD，底面ABCD是∠A=60°，边长为a的菱形，又PD⊥底面ABCD，且PD=CD，点M、N分别是棱AD、PC的中点．
（Ⅰ）证明：PB⊥AC；
（Ⅱ）证明：平面PMB⊥平面PAD；
（Ⅲ）求点A到面PMB的距离．
已知点M是棱长为a的正方体ABCD-A1B1C1D1的棱DD1的中点，则过A，B，M三点的截面积是______．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网