题目内容
设f(x)=x3,等差数列{an}中a3=7,a1+a2+a3=12,记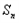 =
=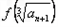 ,令bn=anSn,数列
,令bn=anSn,数列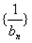 的前n项和为Tn
的前n项和为Tn
(1)求{an}的通项公式和Sn;
(2)求证: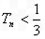 ;
;
(3)是否存在正整数m,n,且1<m<n,使得T1,Tm,Tn成等比数列?若存在,求出m,n的值,若不存在,说明理由.
解:(1)设数列 的公差为
的公差为 ,
,
由 ,
, .解得
.解得 ,
, =3 ,
=3 ,
∴
∵ , ∴Sn=
, ∴Sn= =
= .
.
(2)
∴
∴
(3)由(2)知,
∴ ,
, ,
,
∵ 成等比数列.
成等比数列.
∴ 即
即
当 时,7
时,7 ,
, =1,不合题意;
=1,不合题意;
当 时,
时,
 ,
, =16,符合题意;
=16,符合题意;
当 时,
时,
 ,
, 无正整数解;
无正整数解;
当 时,
时,
 ,
, 无正整数解;
无正整数解;
当 时,
时,
 ,
, 无正整数解;
无正整数解;
当 时,
时,
 ,
, 无正整数解;
无正整数解;
当 时,
时, ,则
,则 ,而
,而 ,所以,此时不存在正整数m,n,且1<m<n,使得
,所以,此时不存在正整数m,n,且1<m<n,使得 成等比数列.
成等比数列.
综上,存在正整数m=2,n=16,且1<m<n,使得 成等比数列.
成等比数列.
.
 的公差为
的公差为 ,
,由
 ,
, .解得
.解得 ,
, =3 ,
=3 , ∴

∵
 , ∴Sn=
, ∴Sn= =
= .
.(2)

∴

∴

(3)由(2)知,

∴
 ,
, ,
,∵
 成等比数列.
成等比数列. ∴
 即
即
当
 时,7
时,7 ,
, =1,不合题意;
=1,不合题意;当
 时,
时,
 ,
, =16,符合题意;
=16,符合题意;当
 时,
时,
 ,
, 无正整数解;
无正整数解;当
 时,
时,
 ,
, 无正整数解;
无正整数解;当
 时,
时,
 ,
, 无正整数解;
无正整数解;当
 时,
时,
 ,
, 无正整数解;
无正整数解;当
 时,
时, ,则
,则 ,而
,而 ,所以,此时不存在正整数m,n,且1<m<n,使得
,所以,此时不存在正整数m,n,且1<m<n,使得 成等比数列.
成等比数列.综上,存在正整数m=2,n=16,且1<m<n,使得
 成等比数列.
成等比数列..

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目