题目内容
已知△ABC的三边长分别为a-2，a，a+2，且它的最大角的正弦值为
，则这个三角形的面积是
- A.
- B.
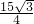
- C.
- D.
B
分析：先确定最大角的度数，再由余弦定理确定a的值，利用三角形的面积公式，即可得到结论．
解答：∵最大角的正弦值为，∴这个角为60°或120°
但这个三角形不是等边三角形，最大角不可能是60°，所以最大角为120°
根据余弦定理（a-2）2+a2-2a（a-2）×（-
）=（a+2）2，解得a=5
∴△ABC的三边长分别为3，5，7
∴这个三角形的面积是
=
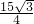
故选B．
点评：本题考查余弦定理的运用，考查三角形面积的计算，确定三角形的边长是关键．
分析：先确定最大角的度数，再由余弦定理确定a的值，利用三角形的面积公式，即可得到结论．
解答：∵最大角的正弦值为
，∴这个角为60°或120° 但这个三角形不是等边三角形，最大角不可能是60°，所以最大角为120°
根据余弦定理（a-2）2+a2-2a（a-2）×（-
）=（a+2）2，解得a=5∴△ABC的三边长分别为3，5，7
∴这个三角形的面积是
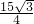
=故选B．
点评：本题考查余弦定理的运用，考查三角形面积的计算，确定三角形的边长是关键．
练习册系列答案
英语小英雄天天默写系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
已知△ABC的三边长为a、b、c，满足直线ax+by+c=0与圆x2+y2=1相离，则△ABC是（ ）
| A、锐角三角形 | B、直角三角形 | C、钝角三角形 | D、以上情况都有可能 |