题目内容
把命题“?x∈R，x2≤0”的否定写在横线上 ．
考点：命题的否定
专题：简易逻辑
分析：直接利用特称命题是否定是全称命题写出结果即可．
解答：
解：因为特称命题的否定是全称命题，所以，命题“?x∈R，x2≤0”的否定是：“?x∈R，x2＞0”．
故答案为：?x∈R，x2＞0．
故答案为：?x∈R，x2＞0．
点评：本题考查命题的否定特称命题与全称命题的否定关系，基本知识的考查．
练习册系列答案
相关题目
计算lg
+
lg5的结果为（ ）
| 2 |
| 1 |
| 2 |
A、
| ||
| B、2 | ||
| C、0 | ||
| D、1 |
设全集U={1，2，3，4，5，6，7，8}，A={1，2，3}，B={3，4，5，6}，则A∩（∁UB）=（ ）
| A、{1，2，3} |
| B、{1，2} |
| C、{1，3} |
| D、{1} |
如图，已知AB为圆O的直径，C为圆O上一点，连接AC并延长使AC=CP，连接PB并延长交圆O于点D，过点P作圆O的切线，切点为E．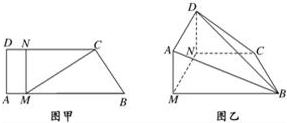
如图甲，直角梯形ABCD中，AB∥CD，∠ADC=90°，点M，N分别在线段AB、CD上，且MN⊥AB，BC=1，MB=2，∠CBM=60°，若梯形ABCD沿MN折起，使DN⊥NC，如图乙．已知{an}是各项均为正数的等比数列，且a1a2013=4，则由bn=log2an，所得数列{bn}的前2013项和为（ ）
| A、1 | ||
| B、2 | ||
C、
| ||
| D、2013 |