题目内容
(本题满分15分)已知数列
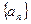 中,
中,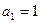 ,
,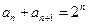 (n∈N*),
(n∈N*),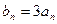
(1)试证数列
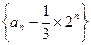 是等比数列,并求数列{
是等比数列,并求数列{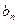 }的通项公式;
}的通项公式;(2)在数列{
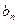 }中,求出所有连续三项成等差数列的项;
}中,求出所有连续三项成等差数列的项;(3)在数列{
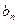 }中,是否存在满足条件1<r<s的正整数r ,s ,使得b1,br,bs成等差数列?若存在,确定正整数r,s之间的关系;若不存在,说明理由.
}中,是否存在满足条件1<r<s的正整数r ,s ,使得b1,br,bs成等差数列?若存在,确定正整数r,s之间的关系;若不存在,说明理由.(1)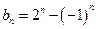 (2)有且仅有连续三项b2,b3,b4成等差数列
(2)有且仅有连续三项b2,b3,b4成等差数列
(3)存在不小于4的正偶数s,且s=r+1,使得b1,br,bs成等差数列
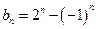 (2)有且仅有连续三项b2,b3,b4成等差数列
(2)有且仅有连续三项b2,b3,b4成等差数列(3)存在不小于4的正偶数s,且s=r+1,使得b1,br,bs成等差数列
解:(1)证明: 由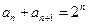 ,得an+1=2n—an,
,得an+1=2n—an,
∴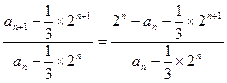
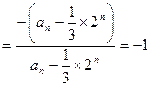 ,
,
∴数列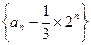 是首项为
是首项为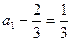 ,公比为
,公比为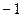 的等比数列.………………3分
的等比数列.………………3分
∴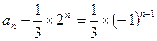 , 即
, 即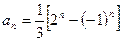 ,
,
∴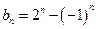 …………………………………………………………………………5分
…………………………………………………………………………5分
(2)解:假设在数列{bn}中,存在连续三项bk-1,bk,bk+1(k∈N*, k≥2)成等差数列,则bk-1+bk+1=2bk,即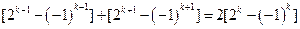 ,
,
即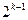 =4
=4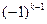 ………………………………………………………………7分
………………………………………………………………7分
若k为偶数,则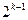 >0,4
>0,4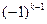 =-4<0,所以,不存在偶数k,使得
=-4<0,所以,不存在偶数k,使得
bk-1,bk,bk+1成等差数列。…………………………………………………………8分
若k为奇数,则k≥3,∴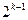 ≥4,而4
≥4,而4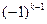 =4,所以,当且仅当k=3时,
=4,所以,当且仅当k=3时,
bk-1,bk,bk+1成等差数列。
综上所述,在数列{bn}中,有且仅有连续三项b2,b3,b4成等差数列。…………10分
(3)要使b1,br,bs成等差数列,只需b1+bs=2 br,
即3+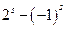 =2[
=2[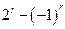 ],即
],即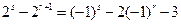 , ①
, ①
(ⅰ)若s=r+1,在①式中,左端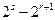 =0,右端
=0,右端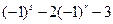 =
=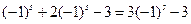 ,要使①式成立,当且仅当s为偶数时成立。又s>r>1,且s,r为正整数,所以,当s为不小于4的正偶数,且s=r+1时,b1,br,bs成等差数列。……………………………………………………………13分
,要使①式成立,当且仅当s为偶数时成立。又s>r>1,且s,r为正整数,所以,当s为不小于4的正偶数,且s=r+1时,b1,br,bs成等差数列。……………………………………………………………13分
(ⅱ)若s≥r+2时,在①式中,左端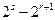 ≥
≥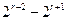 =
=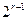 >0,右端
>0,右端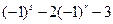 ≤0,∴当s≥r+2时,b1,br,bs不成等差数列。
≤0,∴当s≥r+2时,b1,br,bs不成等差数列。
综上所述,存在不小于4的正偶数s,且s=r+1,使得b1,br,bs成等差数列。…15分
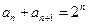 ,得an+1=2n—an,
,得an+1=2n—an,∴
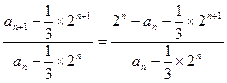
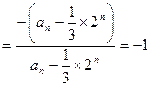 ,
,∴数列
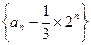 是首项为
是首项为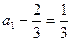 ,公比为
,公比为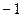 的等比数列.………………3分
的等比数列.………………3分∴
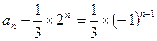 , 即
, 即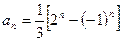 ,
,∴
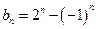 …………………………………………………………………………5分
…………………………………………………………………………5分(2)解:假设在数列{bn}中,存在连续三项bk-1,bk,bk+1(k∈N*, k≥2)成等差数列,则bk-1+bk+1=2bk,即
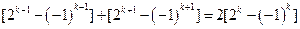 ,
,即
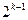 =4
=4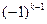 ………………………………………………………………7分
………………………………………………………………7分若k为偶数,则
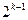 >0,4
>0,4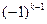 =-4<0,所以,不存在偶数k,使得
=-4<0,所以,不存在偶数k,使得bk-1,bk,bk+1成等差数列。…………………………………………………………8分
若k为奇数,则k≥3,∴
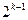 ≥4,而4
≥4,而4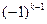 =4,所以,当且仅当k=3时,
=4,所以,当且仅当k=3时,bk-1,bk,bk+1成等差数列。
综上所述,在数列{bn}中,有且仅有连续三项b2,b3,b4成等差数列。…………10分
(3)要使b1,br,bs成等差数列,只需b1+bs=2 br,
即3+
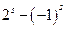 =2[
=2[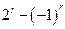 ],即
],即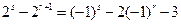 , ①
, ①(ⅰ)若s=r+1,在①式中,左端
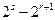 =0,右端
=0,右端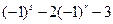 =
=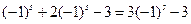 ,要使①式成立,当且仅当s为偶数时成立。又s>r>1,且s,r为正整数,所以,当s为不小于4的正偶数,且s=r+1时,b1,br,bs成等差数列。……………………………………………………………13分
,要使①式成立,当且仅当s为偶数时成立。又s>r>1,且s,r为正整数,所以,当s为不小于4的正偶数,且s=r+1时,b1,br,bs成等差数列。……………………………………………………………13分(ⅱ)若s≥r+2时,在①式中,左端
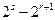 ≥
≥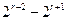 =
=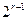 >0,右端
>0,右端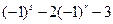 ≤0,∴当s≥r+2时,b1,br,bs不成等差数列。
≤0,∴当s≥r+2时,b1,br,bs不成等差数列。综上所述,存在不小于4的正偶数s,且s=r+1,使得b1,br,bs成等差数列。…15分

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
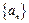 是等差数列,
是等差数列,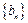 是等比数列,且
是等比数列,且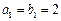 ,
,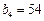 ,
,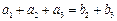 .
.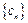 满足
满足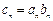 ,求数列
,求数列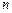 项和
项和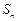 .
. 中,
中, 是它的前
是它的前 项和,并且
项和,并且 ,
, .
. ,求证
,求证 是等比数列
是等比数列 ,求证
,求证 是等差数列
是等差数列 }的前n 项和为
}的前n 项和为 ,已知
,已知 ,
, ,
, 成等差数列
成等差数列 -
- =3,求
=3,求

 中,又
中,又 成等比数列,则
成等比数列,则 __________
__________ 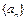 中,前n项和
中,前n项和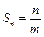 ,前m项和
,前m项和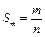 ,其中
,其中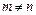 ,则
,则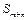 的值( )
的值( ) 为其前n项和,且
为其前n项和,且 则
则 = .
= . 的函数
的函数 满足
满足 ,
,
 ,若
,若 成等差数列,则
成等差数列,则 的值为 .
的值为 .