Question

【题目】如图在四面体中，是边长为2的等边三角形，为直角三角形，其中为直角顶点，.分别是线段上的动点，且四边形为平行四边形.

（1）求证：平面，平面；

（2）试探究当二面角从0°增加到90°的过程中，线段在平面上的投影所扫过的平面区域的面积；

（3）设，且为等腰三角形，当为何值时，多面体的体积恰好为？

Answer 1

【答案】（1）见解析 （2） （3）

【解析】

（1）先通过线面平行的判定定理，证得平面，通过线面平行的性质定理，证得，由此证得平面；同理证得平面.

（2）画出为、时的投影，由此判断出线段在平面上的投影所扫过的平面区域，进而求得区域的面积.

（3）先求得三棱锥的面积为，通过分割的方法，得到，分别求得与的关系式，再由列方程，解方程求得的值.

（1）∵四边形为平行四边形，

∴．而面，面，

∴面．而面，面面，

∴∥．而面，面，

∴∥平面．同理，∥平面；

（2）∵，

∴在平面上的投影满足，即在线段的中垂线上．

如图所示，将补成边长为的正，

当二面角为角时，即点在平面上，此时为，

当二面角为角时，此时为中点，

故在平面上的投影所扫过的平面区域为，而，

故线段在平面上的投影所扫过的平面区域的面积为；

（3）∵，，且为等腰三角形，∴．

取中点，易得：，，，

满足：，根据勾股定理可知．

∴平面．∴．

而多面体的体积恰好为，即多面体的体积恰为四面体体积的一半．

连接．

，∴．

，∴．

∴，

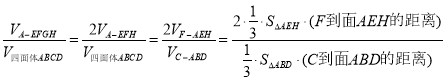
∴，整理：，即，

解得：（舍去）．