题目内容
已知圆C：x2+（y-1）2=1和圆C1：（x-2）2+（y-1）2=1，现在构造一系列的圆C1，C2，C3，…，Cn，…，使圆Cn+1同时与Cn和圆C都相切，并都与OX轴相切．回答：（1）求圆Cn的半径rn；
（2）证明：两个相邻圆Cn-1和Cn在切点间的公切线长为
；（3）求和
．
【答案】分析：（1）利用ECn-1=AB=ACn+BCn，建立等式，可得{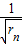
}成等差数列，由此可得结论；
（2）利用勾股定理可求两个相邻圆Cn-1和Cn在切点间的公切线长；
（3）利用裂项法求和，再求极限即可．
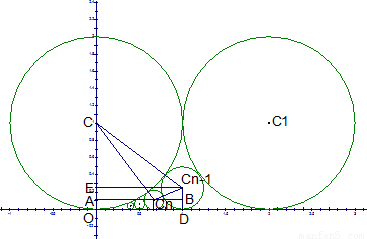
解答：（1）解：如图，在直角梯形ODCn-1C中，AC=1-rn，CCn=1+rn，CCn-1=1+rn-1，CnCn-1=rn+rn-1．Cn-1B=rn-1-rn．…（2分）
∴有ACn=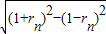
，
，
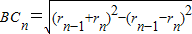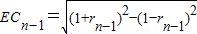，ECn-1=AB=ACn+BCn
∴
∴
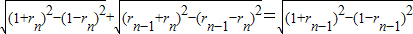
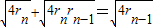．即
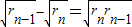．…（4分）
由此可得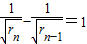
．
∴{
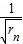}成等差数列，…（6分）
∵r1=1，∴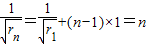
，∴
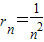．…（8分）
（2）证明：公切线长为ln=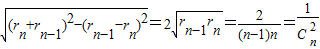
．…（11分）
（3）解：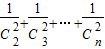
=
=
．
∴
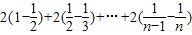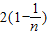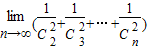=2．…（14分）
点评：本题考查等差数列的判定，考查数列的通项与求和，考查直线与圆的位置关系，考查极限的求解，属于中档题．
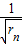}成等差数列，由此可得结论；（2）利用勾股定理可求两个相邻圆Cn-1和Cn在切点间的公切线长；
（3）利用裂项法求和，再求极限即可．
解答：（1）解：如图，在直角梯形ODCn-1C中，AC=1-rn，CCn=1+rn，CCn-1=1+rn-1，CnCn-1=rn+rn-1．Cn-1B=rn-1-rn．…（2分）
∴有ACn=
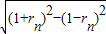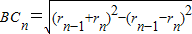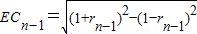，，，ECn-1=AB=ACn+BCn∴
∴
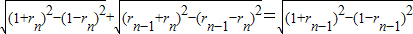
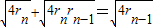．即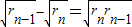．…（4分）由此可得
．∴{
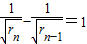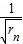}成等差数列，…（6分）∵r1=1，∴
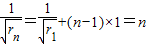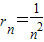，∴．…（8分）（2）证明：公切线长为ln=
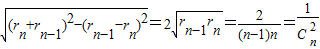．…（11分）（3）解：
==．∴
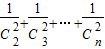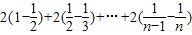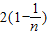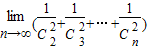=2．…（14分）点评：本题考查等差数列的判定，考查数列的通项与求和，考查直线与圆的位置关系，考查极限的求解，属于中档题．
练习册系列答案
相关题目