题目内容
已知向量 =(-1,2),
=(-1,2), =(1,3),
=(1,3), =(3,m).
=(3,m).
(1)若点A,B,C能构成三角形,求实数m应满足的条件;
(2)若点A,B,C构成直角三角形,且∠B=90°,求∠ACO的余弦值.
解:(1)∵ =(-1,2),
=(-1,2), =(1,3),
=(1,3), =(3,m).
=(3,m).
∴ =
= -
- =(2,1),
=(2,1), =
= -
- =(2,m-3)
=(2,m-3)
∵点A,B,C能构成三角形,
∴向量 、
、 不能共线,得2(m-3)≠1×2,所以m≠4,
不能共线,得2(m-3)≠1×2,所以m≠4,
即m满足的条件是m≠4
(2)∵ =(2,1),
=(2,1), =(2,m-3)且△ABC是以B为直角顶点的直角三角形
=(2,m-3)且△ABC是以B为直角顶点的直角三角形
∴ •
• =2×2+1×(m-3)=0,解得m=-1
=2×2+1×(m-3)=0,解得m=-1
可得 =(3,-1),
=(3,-1),
∴ =
= -
- =(-4,3),
=(-4,3),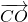 =-
=- =(-3,1),
=(-3,1),
此时,cos∠ACO= =
= =
= ,
,
∴∠ACO的余弦值等于 .
.
分析:(1)因为A,B,C能构成三角形,所以向量 、
、 不共线.算出向量
不共线.算出向量 、
、 的坐标,根据向量共线的条件列式,解之即可得到实数m应满足的条件;
的坐标,根据向量共线的条件列式,解之即可得到实数m应满足的条件;
(2)由向量 与
与 垂直,列出关于m的方程,解之得m=-1.进而得到向量
垂直,列出关于m的方程,解之得m=-1.进而得到向量 、
、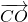 的坐标,利用向量的夹角公式进行计算,即可得到∠ACO的余弦值.
的坐标,利用向量的夹角公式进行计算,即可得到∠ACO的余弦值.
点评:本题给出A、B、C三点能构成三角形,求参数m的取值范围,着重考查了平面向量共线的充要条件和向量数量积运算性质等知识,属于中档题.
 =(-1,2),
=(-1,2), =(1,3),
=(1,3), =(3,m).
=(3,m).∴
 =
= -
- =(2,1),
=(2,1), =
= -
- =(2,m-3)
=(2,m-3)∵点A,B,C能构成三角形,
∴向量
 、
、 不能共线,得2(m-3)≠1×2,所以m≠4,
不能共线,得2(m-3)≠1×2,所以m≠4,即m满足的条件是m≠4
(2)∵
 =(2,1),
=(2,1), =(2,m-3)且△ABC是以B为直角顶点的直角三角形
=(2,m-3)且△ABC是以B为直角顶点的直角三角形∴
 •
• =2×2+1×(m-3)=0,解得m=-1
=2×2+1×(m-3)=0,解得m=-1可得
 =(3,-1),
=(3,-1),∴
 =
= -
- =(-4,3),
=(-4,3),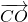 =-
=- =(-3,1),
=(-3,1),此时,cos∠ACO=
 =
= =
= ,
,∴∠ACO的余弦值等于
 .
.分析:(1)因为A,B,C能构成三角形,所以向量
 、
、 不共线.算出向量
不共线.算出向量 、
、 的坐标,根据向量共线的条件列式,解之即可得到实数m应满足的条件;
的坐标,根据向量共线的条件列式,解之即可得到实数m应满足的条件;(2)由向量
 与
与 垂直,列出关于m的方程,解之得m=-1.进而得到向量
垂直,列出关于m的方程,解之得m=-1.进而得到向量 、
、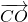 的坐标,利用向量的夹角公式进行计算,即可得到∠ACO的余弦值.
的坐标,利用向量的夹角公式进行计算,即可得到∠ACO的余弦值.点评:本题给出A、B、C三点能构成三角形,求参数m的取值范围,着重考查了平面向量共线的充要条件和向量数量积运算性质等知识,属于中档题.

练习册系列答案
 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案
相关题目
已知向量
=(1,2),
=(x,2),则向量
+2
与2
-
( )
| a |
| b |
| a |
| b |
| a |
| b |
| A、垂直的必要条件是x=-2 | ||
B、垂直的充要条件是x=
| ||
| C、平行的充分条件是x=-2 | ||
| D、平行的充要条件是x=1 |