题目内容
已知四棱锥P-ABCD的底面ABCD是边长为2的正方形，PD⊥底面ABCD，E，F分别为棱BC，AD的中点.
（Ⅰ）求证：DE∥平面PFB；
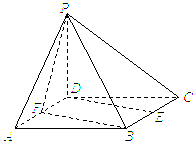（Ⅱ）已知二面角P-BF-C的余弦值为
，求四棱锥P-ABCD的体积.
（Ⅱ）
解析:
（Ⅰ）因为E，F分别为正方形ABCD的两边BC，AD的中点，
所以
, 所以，
为平行四边形, ……………….2分
得
， ……………….3分
又因为
平面PFB，且
平面PFB, ……………….4分
所以DE∥平面PFB. ……………….5分
（Ⅱ）如图，以D为原点，射线DA,DC,DP分
别为x,y,z轴建立空间直角坐标系.设PD=a,
可得如下点的坐标：
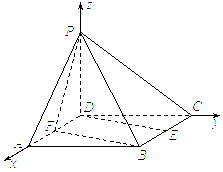P(0,0,a),F(1,0,0),B(2,2,0)
则有：
……………….6分
因为PD⊥底面ABCD，所以平面ABCD的
一个法向量为
， ……………….7分
设平面PFB的一个法向量为
，则可得
即 
令x=1,得
，所以
. ……………….9分
由已知，二面角P-BF-C的余弦值为，所以得:
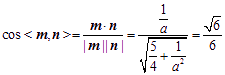, ……………….10分
解得a =2. ……………….11分
因为PD是四棱锥P-ABCD的高，
所以，其体积为
通城学典默写能手系列答案
如图，已知四棱锥P--ABC的底面ABCD为正方形，PA⊥平面ABCD，PA=AB=2，e为PC的中点，F为AD的中点．
如图，已知四棱锥P-ABCD的底面是直角梯形，∠ABC=∠BCD=90°，AB=BC=2CD=2，PB=PC，侧面PBC⊥底面ABCD，O是BC的中点．
已知四棱锥P-ABCD的底面是直角梯形，∠ABC=∠BCD=90°，E为BC中点，AE与BD交于O点，AB=BC=2CD=2，BD⊥PE．
如图，已知四棱锥P-ABCD中，PA⊥平面ABCD，底面ABCD是直角梯形，∠DAB=∠ABC=90°，E是线段PC上一点，PC⊥平面BDE．