题目内容
函数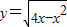
的单调递减区间为 ．
【答案】分析：先确定函数的定义域，再确定内函数的单调递减区间，即可求得结论．
解答：解：先求函数的定义域：4x-x2≥0，∴0≤x≤4，即定义域为[0，4]
∵t=4x-x2=-（x-2）2+4的单调递减区间为[2，+∞）
∴函数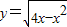
的单调递减区间为[2，4]
故答案为：[2，4]
点评：本题考查复合函数的单调性，解题的关键是先确定函数的定义域，再确定内函数的单调递减区间，属于中档题．
解答：解：先求函数的定义域：4x-x2≥0，∴0≤x≤4，即定义域为[0，4]
∵t=4x-x2=-（x-2）2+4的单调递减区间为[2，+∞）
∴函数
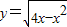的单调递减区间为[2，4]故答案为：[2，4]
点评：本题考查复合函数的单调性，解题的关键是先确定函数的定义域，再确定内函数的单调递减区间，属于中档题．
练习册系列答案
相关题目
上任一点
处的切线斜率
，则该函数的单调递减区间为 ．
的单调递减区间为____________,增区间为_______________.