题目内容
已知函数 an=f(n),n∈N*,{an}是递增数列,则实数a的取值范围是 .
an=f(n),n∈N*,{an}是递增数列,则实数a的取值范围是 .
【答案】分析:由题设知当1≤n≤6时,an=(3-a)n-3;当n>6时,an=an-6.再由{an}是递增数列,建立不等式组 ,由此能求出实数a的取值范围.
,由此能求出实数a的取值范围.
解答:解:∵函数 ,
,
an=f(n),n∈N*,
∴当1≤n≤6时,an=(3-a)n-3;
当n>6时,an=an-6.
∵{an}是递增数列,
∴ ,
,
解得 .
.
故答案为:( ).
).
点评:本题考查数列与函数的综合,易错点是忽视a7>a6,导致出错.解题时要认真审题,注意分段函数的性质和应用.
 ,由此能求出实数a的取值范围.
,由此能求出实数a的取值范围.解答:解:∵函数
 ,
,an=f(n),n∈N*,
∴当1≤n≤6时,an=(3-a)n-3;
当n>6时,an=an-6.
∵{an}是递增数列,
∴
 ,
,解得
 .
.故答案为:(
 ).
).点评:本题考查数列与函数的综合,易错点是忽视a7>a6,导致出错.解题时要认真审题,注意分段函数的性质和应用.

练习册系列答案
相关题目
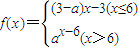 an=f(n),n∈N*,{an}是递增数列,则实数a的取值范围是 .
an=f(n),n∈N*,{an}是递增数列,则实数a的取值范围是 .