题目内容
已知函数f（x）=x2+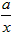
（x≠0，常数a∈R），若函数f（x）在x∈ [2，+∞）上是单调递增的，求a的取值范围。
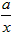（x≠0，常数a∈R），若函数f（x）在x∈ [2，+∞）上是单调递增的，求a的取值范围。解：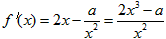
，要使f（x）在[2，+∞）上是单调递增的，
则f′（x）≥0在x∈[2，+∞）时恒成立，
即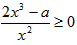
在x∈[2，+∞）时恒成立，
∵x2＞0，
∴2x3-a≥0，
∴a≤2x3在x∈[2，+∞）上恒成立，
∴a≤（2x3）min，
∵x∈ [2，+∞），y=2x3是单调递增的，
∴（2x3）min=16，
∴a≤16，当a=16时，有且只有f′（2）=0，
∴a的取值范围是a≤16。
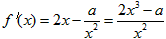，要使f（x）在[2，+∞）上是单调递增的，则f′（x）≥0在x∈[2，+∞）时恒成立，
即
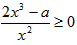在x∈[2，+∞）时恒成立，∵x2＞0，
∴2x3-a≥0，
∴a≤2x3在x∈[2，+∞）上恒成立，
∴a≤（2x3）min，
∵x∈ [2，+∞），y=2x3是单调递增的，
∴（2x3）min=16，
∴a≤16，当a=16时，有且只有f′（2）=0，
∴a的取值范围是a≤16。
练习册系列答案
阅读快车系列答案
相关题目
已知函数f（x）=Asin（ωx+φ）（x∈R，A＞0，ω＞0，|φ|＜| π |
| 2 |
A、f(x)=2sin(πx+
| ||
B、f(x)=2sin(2πx+
| ||
C、f(x)=2sin(πx+
| ||
D、f(x)=2sin(2πx+
|