题目内容
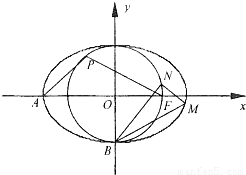
已知椭圆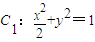 和圆
和圆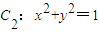 ,左顶点和下顶点分别为A,B,且F是椭圆C1的右焦点.
,左顶点和下顶点分别为A,B,且F是椭圆C1的右焦点.(1)若点P是曲线C2上位于第二象限的一点,且△APF的面积为
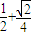 ,求证:AP⊥OP;
,求证:AP⊥OP;(2)点M和N分别是椭圆C1和圆C2上位于y轴右侧的动点,且直线BN的斜率是直线BM斜率的2倍,求证:直线MN恒过定点.
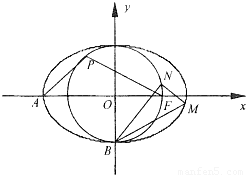
【答案】分析:(1)设曲线C2上的点P(x,y),利用△APF的面积为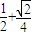 ,可求P的坐标,计算
,可求P的坐标,计算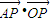 =0,即可证得结论;
=0,即可证得结论;
(2)设直线BM、BN的方程为y=2kx-1,代入椭圆方程,求得M,N的坐标,计算直线MN的斜率,可得直线MN的方程,即可求得结论.
解答:证明:(1)设曲线C2上的点P(x,y),且x<0,y>0,由题意A(- ,0),F(1,0)
,0),F(1,0)
∵△APF的面积为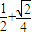 ,∴
,∴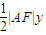 =
=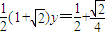
∴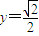 ,
,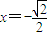
∴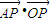 =
=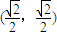 •
•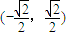 =0
=0
∴AP⊥OP;
(2)设直线BM的斜率为k,则直线BN的斜率为2k,又两直线都过点B(0,-1)
∴直线BM的方程为y=kx-1,直线BN的方程为y=2kx-1
将y=kx-1代入椭圆方程,消元可得(1+2k2)x2-4kx=0,∴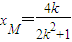 ,∴
,∴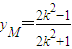
∴M(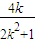 ,
,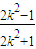 )
)
同理N(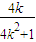 ,
, )
)
∴直线MN的斜率为 =-
=-
∴直线MN的方程为y-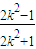 =-
=-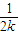 (x-
(x-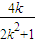 )
)
整理得y=-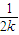 x+1
x+1
∴直线MN恒过定点(0,1)
点评:本题考查椭圆与圆的标准方程,考查直线与椭圆的位置关系,考查直线恒过定点,确定点的坐标是关键.
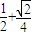 ,可求P的坐标,计算
,可求P的坐标,计算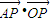 =0,即可证得结论;
=0,即可证得结论;(2)设直线BM、BN的方程为y=2kx-1,代入椭圆方程,求得M,N的坐标,计算直线MN的斜率,可得直线MN的方程,即可求得结论.
解答:证明:(1)设曲线C2上的点P(x,y),且x<0,y>0,由题意A(-
 ,0),F(1,0)
,0),F(1,0)∵△APF的面积为
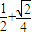 ,∴
,∴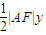 =
=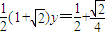
∴
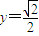 ,
,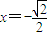
∴
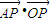 =
=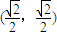 •
•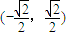 =0
=0∴AP⊥OP;
(2)设直线BM的斜率为k,则直线BN的斜率为2k,又两直线都过点B(0,-1)
∴直线BM的方程为y=kx-1,直线BN的方程为y=2kx-1
将y=kx-1代入椭圆方程,消元可得(1+2k2)x2-4kx=0,∴
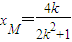 ,∴
,∴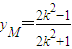
∴M(
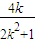 ,
,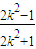 )
)同理N(
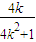 ,
, )
)∴直线MN的斜率为
 =-
=-
∴直线MN的方程为y-
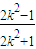 =-
=-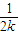 (x-
(x-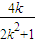 )
)整理得y=-
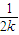 x+1
x+1∴直线MN恒过定点(0,1)
点评:本题考查椭圆与圆的标准方程,考查直线与椭圆的位置关系,考查直线恒过定点,确定点的坐标是关键.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
 的左、右焦点分别为F1、F2,上顶点为A,△AF1F2为正三角形,且以线段F1F2为直径的圆与直线
的左、右焦点分别为F1、F2,上顶点为A,△AF1F2为正三角形,且以线段F1F2为直径的圆与直线 相切.
相切. 的对称点,动点M满足
的对称点,动点M满足 . 问是否存在一个定点T,使得动点M到定点T的距离为定值?若存在,求出定点T的坐标及此定值;若不存在,请说明理由.
. 问是否存在一个定点T,使得动点M到定点T的距离为定值?若存在,求出定点T的坐标及此定值;若不存在,请说明理由.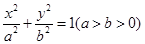 ,
,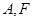 是其左顶点和左焦点,
是其左顶点和左焦点,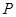 是圆
是圆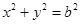 上的动点,若
上的动点,若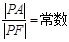 ,则此椭圆的离心率是
,则此椭圆的离心率是  已知椭圆
已知椭圆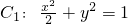 和圆
和圆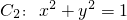 ,左顶点和下顶点分别为A,B,且F是椭圆C1的右焦点.
,左顶点和下顶点分别为A,B,且F是椭圆C1的右焦点.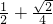 ,求证:AP⊥OP;
,求证:AP⊥OP;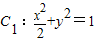 和圆
和圆 ,左顶点和下顶点分别为A,B,且F是椭圆C1的右焦点.
,左顶点和下顶点分别为A,B,且F是椭圆C1的右焦点. ,求证:AP⊥OP;
,求证:AP⊥OP;