题目内容
已知函数 .
.
(1)求函数 上的最大值和最小值.
上的最大值和最小值.
(2)在锐角△ABC中, 求△ABC的面积.
求△ABC的面积.
解:(1)
= .(2分)
.(2分)
∵ ,∴
,∴ ,
,
∴ ,
,
∴ ,
,
∴f(x)最大值为2,最小值为 .(6分)
.(6分)
(2)由 得
得 ,
,
∵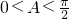 ,则
,则 ,
,
∴ ,∴
,∴ .(8分)
.(8分)
由余弦定理 ,
,
∴c2-2c-3=0,解得c=3或-1(舍去),
故c=3,(10分)
∴△ABC的面积S= .(12分)
.(12分)
分析:(1)先将函数利用降幂扩角公式,利用辅助角公式化简,再整体思考,利用正弦函数的性质,即可求得函数 上的最大值和最小值;
上的最大值和最小值;
(2)由 得
得 ,从而可求A,再利用余弦定理求边,进而利用面积公式可求△ABC的面积
,从而可求A,再利用余弦定理求边,进而利用面积公式可求△ABC的面积
点评:本题将三角函数与解三角形综合,考查三角函数的性质,考查三角恒等变换,考查余弦定理的运用,有综合性.

=
 .(2分)
.(2分)∵
 ,∴
,∴ ,
,∴
 ,
,∴
 ,
,∴f(x)最大值为2,最小值为
 .(6分)
.(6分)(2)由
 得
得 ,
,∵
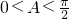 ,则
,则 ,
,∴
 ,∴
,∴ .(8分)
.(8分)由余弦定理
 ,
,∴c2-2c-3=0,解得c=3或-1(舍去),
故c=3,(10分)
∴△ABC的面积S=
 .(12分)
.(12分)分析:(1)先将函数利用降幂扩角公式,利用辅助角公式化简,再整体思考,利用正弦函数的性质,即可求得函数
 上的最大值和最小值;
上的最大值和最小值;(2)由
 得
得 ,从而可求A,再利用余弦定理求边,进而利用面积公式可求△ABC的面积
,从而可求A,再利用余弦定理求边,进而利用面积公式可求△ABC的面积点评:本题将三角函数与解三角形综合,考查三角函数的性质,考查三角恒等变换,考查余弦定理的运用,有综合性.

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目





 ,如果满足;对任意
,如果满足;对任意 ,存在常数
,存在常数 ,都有
,都有 成立,则称
成立,则称 ,
,
 时,求函数
时,求函数 上的值域,并判断函数
上的值域,并判断函数 上是以3为上界函数值,求实数
上是以3为上界函数值,求实数 的取值范围;
的取值范围; ,求函数
,求函数 在
在 上的上界T的取值范围。
上的上界T的取值范围。 .
. 上的函数值的取值范围.
上的函数值的取值范围. .
. 上的函数值的取值范围.
上的函数值的取值范围.