Question

以长方体ABCD-A₁B₁C₁D₁的六条面对角线为棱，可以构成四面体A-B₁CD₁，A₁-BC₁D，若这两个四面体组合起来的体积为1（重合部分只算一次），则长方体的体积（　　）

• A．2
• B．

  7

  3

• C．3
• D．4

Answer 1

分析：先画出图形，设长方体的体积为V，然后求出除两个四面体组合以外的体积，从而求出两个四面体组合的体积，建立等式解之即可求出所求．

解答：解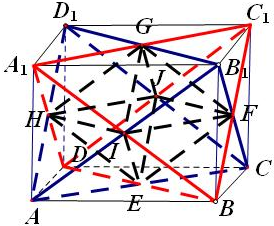：先画出图形，设长方体的体积为V
观察底面上除两个四面体组合以外有4个三棱锥，
V三棱锥I-ABE=

1

3

×

1

4

×

1

2

V=

V

24

V三棱锥F-BCE=

1

3

×

1

4

×

1

2

V=

V

24

V三棱锥J-CDE=

1

3

×

1

4

×

1

2

V=

V

24

V三棱锥H-ADE=

1

3

×

1

4

×

1

2

V=

V

24

同理每个面上有4个，一共有6个面，而三棱锥I-ABE与三棱锥E-ABI是同一个三棱锥，共有12个三棱锥
则除两个四面体组合以外的体积为

V

24

×12=

V

2

∴两个四面体组合的体积为V-

V

2

=1
则V=2
故选A．

点评：本题主要考查了棱锥的体积，以及组合体的体积，解决此类问题常常用割补法，属于中档题．