题目内容
如图棱长是1的正方体，P、Q分别是棱AB、CC1上的点，且
=
=2．
（1）求证：A1P⊥平面AQD；
（2）求直线PQ与平面AQD所成角的正弦值．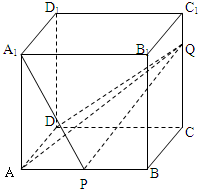
| AP |
| PB |
| CQ |
| QC1 |
（1）求证：A1P⊥平面AQD；
（2）求直线PQ与平面AQD所成角的正弦值．
证明：（1）平面AQD与侧棱B1B的交点是R，
显然
=2，在正方形ABB1A1中
由
=
=2可得△A1AP≌△ABR
所以AR⊥A1P，
又AA1⊥平面ABCD，AP⊥AD，得A1P⊥AD，
∴A1P⊥平面AQD
（2）设A1P与AR交于点S，连接SQ，则∠PQS=θ即为PQ与平面AQD所成角．
在Rt△PQS中，|PS|=
，|PQ|=
，∴sinθ=
=
=
，
即直线PQ与平面AQD所成角的正弦值是
．
显然
| BR |
| RB1 |
由
| AP |
| PB |
| BR |
| RB1 |
所以AR⊥A1P，
又AA1⊥平面ABCD，AP⊥AD，得A1P⊥AD，
∴A1P⊥平面AQD
（2）设A1P与AR交于点S，连接SQ，则∠PQS=θ即为PQ与平面AQD所成角．
在Rt△PQS中，|PS|=
| 4 | ||
3
|
| ||
| 3 |
| |PS| |
| |PQ| |
| 4 | ||
|
2
| ||
| 91 |
即直线PQ与平面AQD所成角的正弦值是
2
| ||
| 91 |
练习册系列答案
相关题目
如图棱长是1的正方体，P、Q分别是棱AB、CC1上的点，且
如图棱长是1的正方体，P、Q分别是棱AB、CC1上的点，且
．