题目内容
当a+b+c=0时，直线ax+by+c=0必过定点________．
（1，1）
分析：由于a+b+c=0，故点（1，1）满足直线方程ax+by+c=0，即点（1，1）在直线ax+by+c=0上，由此得出结论．
解答：由于a+b+c=0，故点（1，1）满足直线方程ax+by+c=0，即点（1，1）在直线ax+by+c=0上，即直线ax+by+c=0必过定点（1，1），
故答案为 （1，1）．
点评：本题主要考查直线过定点问题，属于基础题．
分析：由于a+b+c=0，故点（1，1）满足直线方程ax+by+c=0，即点（1，1）在直线ax+by+c=0上，由此得出结论．
解答：由于a+b+c=0，故点（1，1）满足直线方程ax+by+c=0，即点（1，1）在直线ax+by+c=0上，即直线ax+by+c=0必过定点（1，1），
故答案为 （1，1）．
点评：本题主要考查直线过定点问题，属于基础题．
练习册系列答案
相关题目
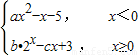若x＞0，且点A（x，f（x））关于坐标原点的对称点也在f（x）的图象上，则称x为f（x）的一个“靓点”．
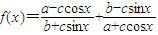，其中a、b、c为正实数，
．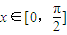