题目内容

平行四边形ABCD中，已知：
DE
=
1
3
DC
，
DF
=
1
4
DB
，求证：A、E、F三点共线．
分析：证明一：（利用共线向量的判定定理证明）以
AB
，
BD
作为基底，推出
AE
=
4
3
AF
，得到A、E、F共线．
证明二：（利用三点共线的判定定理证明）推出
DF
=
1
4
DA
+
3
4
DE
，通过
1
4
+
3
4
=1，说明A、E、F共线
解答：证明：证明一：（利用共线向量的判定定理证明）
以
AB
，
BD
作为基底，
有：
AF
=
AB
+
BF
=
AB
+
3
4
BD
，
AE
=
AD
+
DE
=
AB
+
BD
+
1
3
AB
=
4
3
AB
+
BD
，
从而
AE
=
4
3
AF
，所以A、E、F共线．
证明二：（利用三点共线的判定定理证明）
DF
=
1
4
DB
=
1
4
(
DA
+
DC
)=
1
4
(
DA
+3
DE
)=
1
4
DA
+
3
4
DE
，
而：
1
4
+
3
4
=1，所以A、E、F共线．
（可以建立坐标系，利用求出等比分点坐标公式求出E、F的坐标，再证明A、E、F共线）
点评：本题考查共线向量的判定定理，三点共线的判定定理证明问题的方法，考查计算能力，定理的应用能力．
练习册系列答案
相关题目
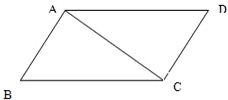精英家教网如图，在平行四边形ABCD中，AB=AC=1，∠ACD=90°，将它沿对角线AC折起，使AB与CD成60°角，则此时B、D的距离是 （　　）
A、2或
3
B、2或
2
C、2
D、1或
2
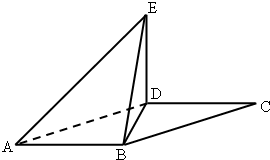精英家教网如图，平行四边形ABCD中，∠DAB=60°，AB=2，AD=4将△CBD沿BD折起到△EBD的位置，使平面EDB⊥平面ABD．
（I）求证：AB⊥DE
（Ⅱ）求三棱锥E-ABD的侧面积．
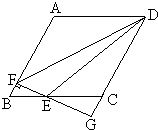精英家教网如图，在平行四边形ABCD中，AB=4，BC=3，∠BAD=120°，E为BC上一动点（不与B重合），作EF⊥AB于F，FE的延长线交DC的延长线于点G，设BE=x，△DEF的面积为S．
（1）求证：△BEF∽△CEG；
（2）求用x表示S的函数关系式，并写出x的取值范围；
（3）当E运动到何处时，S有最大值，最大值是多少？
（2012•广州二模）在平行四边形ABCD中，点E是AD的中点，BE与AC相交于点F，若
EF
=m
AB
+n
AD
(m，n∈R)，则
m
n
的值为
-2
-2
．
（2011•天津模拟）在平行四边形ABCD中，
AE
=
1
3
AB
，
AF
=
1
4
AD
，CE与BF相交于G点．若
AB
=
a
，
AD
=
b
，则
AG
=（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网