题目内容
(本小题满分14分)如图,在三棱锥P- ABC中,已知平面PBC  平面ABC.
平面ABC.

(1)若AB BC,CP
BC,CP PB,求证:CP
PB,求证:CP PA:
PA:
(2)若过点A作直线 ⊥平面ABC,求证:
⊥平面ABC,求证: //平面PBC.
//平面PBC.
(1)详见解析,(2)详见解析
【解析】
试题分析:(1)先根据面面垂直性质定理,将条件平面 ⊥平面
⊥平面 转化为线面垂直:
转化为线面垂直: ⊥平面
⊥平面 ,从而
,从而 ⊥
⊥ .又因为
.又因为 ⊥
⊥ ,所以
,所以 ⊥平面
⊥平面 ,从而
,从而 ⊥
⊥ .(2)证明线面平行,一般利用线面平行判定定理进行证明,关键找出线线平行.本题可从线面垂直出发找平行关系:在平面
.(2)证明线面平行,一般利用线面平行判定定理进行证明,关键找出线线平行.本题可从线面垂直出发找平行关系:在平面 内过点
内过点 作
作 ⊥
⊥ ,根据面面垂直性质定理,将条件平面
,根据面面垂直性质定理,将条件平面 ⊥平面
⊥平面 转化为线面垂直:
转化为线面垂直: ⊥平面
⊥平面 .又
.又 ⊥平面
⊥平面 ,所以
,所以 //
// ,从而
,从而 //平面
//平面 .
.
试题解析:(1)因为平面 ⊥平面
⊥平面 ,平面
,平面
 平面
平面
 ,
, 平面
平面 ,
,
 ⊥
⊥ ,所以
,所以 ⊥平面
⊥平面 . 2分
. 2分
因为 平面
平面 ,所以
,所以 ⊥
⊥ . 4分
. 4分
又因为 ⊥
⊥ ,且
,且 ,
, 平面
平面 ,
,
所以 ⊥平面
⊥平面 , 6分
, 6分
又因为 平面
平面 ,所以
,所以 ⊥
⊥ . 7分
. 7分
(2)在平面 内过点
内过点 作
作 ⊥
⊥ ,垂足为
,垂足为 . 8分
. 8分
因为平面 ⊥平面
⊥平面 ,又平面
,又平面 ∩平面
∩平面 =BC,
=BC,
 平面
平面 ,所以
,所以 ⊥平面
⊥平面 . 10分
. 10分
又 ⊥平面
⊥平面 ,所以
,所以 //
// . 12分
. 12分
又 平面
平面 ,
, 平面
平面 ,
, //平面
//平面 . 14分
. 14分

考点:面面垂直性质定理,线面平行判定定理

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,若函数
,若函数 有三个不同的零点,则实数
有三个不同的零点,则实数 的取值范围是 .
的取值范围是 . 中,角
中,角 、
、 、
、 所对的边分别为
所对的边分别为 、
、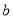 、
、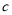 ,若
,若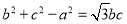 ,且
,且 ,则下列关系一定不成立的是( )
,则下列关系一定不成立的是( ) B.
B.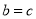 C.
C. D.
D.
 ,
, ,
, ,则
,则 ,
, ,
, 的大小关系为( )
的大小关系为( ) B.
B. C.
C. D.
D.
 ,集合
,集合 ,则
,则 等于( )
等于( ) B.
B. C.
C. D.
D.
 的图象分别向左、向右各平移
的图象分别向左、向右各平移 个单位长度后,所得的两个图象对称轴重合,则
个单位长度后,所得的两个图象对称轴重合,则  的最小值为______.
的最小值为______. ,则不等式
,则不等式  的解集为______.
的解集为______. 的参数方程为
的参数方程为 (
( 为参数),圆C的参数方程为
为参数),圆C的参数方程为 (
( 为参数).若直线
为参数).若直线