题目内容
【题目】甲、乙两人进行围棋比赛，约定先连胜两局者直接赢得比赛．若赛完5局仍未出现连胜，则判定获胜局数多者赢得比赛．假设每局甲获胜的概率为
，乙获胜的概率为
各局比赛结果相互独立．则甲在4局以内（含4局）赢得比赛的概率为（ ）
A.
B.
C.
D.
【答案】A
【解析】
甲在4局内（含4局）赢得比赛包含3种情况：①甲胜第1、2局；②乙胜第1局，甲胜2、3局；③甲胜第1局，乙胜第2局，甲胜第3、4局，由此可求得甲在4局以内（含4局）赢得比赛的概率.
由题意，甲在4局内（含4局）赢得比赛包含3种情况：
①甲胜第1、2局，概率为
；
②乙胜第1局，甲胜2、3局，概率为
；
③甲胜第1局，乙胜第2局，甲胜第3、4局，概率为
，
所以甲在4局以内（含4局）赢得比赛的概率为
.
故选：A.
练习册系列答案
相关题目
【题目】某种新产品投放市场一段时间后，经过调研获得了时间
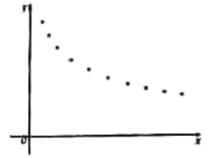
（天数）与销售单价
（元）的一组数据，且做了一定的数据处理（如表），并作出了散点图（如图）.
|
|
|
|
|
|
|
1.63 | 37.8 | 0.89 | 5.15 | 0.92 |
| 18.40 |
表中
.
（1）根据散点图判断，
与
哪一个更适合作价格关于时间的回归方程类型？（不必说明理由）
（2）根据判断结果和表中数据，建立关于的回归方程.
（3）若该产品的日销售量
（件）与时间的函数关系为
，求该产品投放市场第几天的销售额最高？最高为多少元？
附：对于一组数据
，其回归直线
的斜率和截距的最小二乘法估计分别为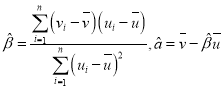
.
