Question

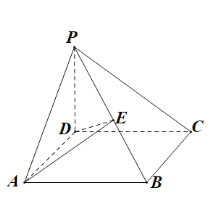
【题目】如图，在三棱锥中，，，，，，分别为线段，上的点，且，.

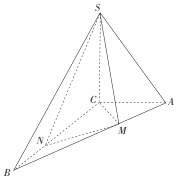
（1）证明：；

（2）若，求二面角的余弦值.

Answer 1

【答案】（1）见证明；（2）

【解析】

（1）证明BC⊥平面SAC，即可推出SC⊥平面ABC，从而得到MN⊥平面SCM，即可证明MN⊥SM．（2）以C为原点，以，，为轴，轴，轴的正方向建立空间直角坐标系，求出平面SAM和平面SMN的法向量，利用空间向量的夹角的余弦，求解二面角A﹣SM﹣N的余弦值．

（1）证明：由，，且，则平面，

平面，故，又，，则平面，

平面，故.

因为，，所以，故.

又因为，所以平面.

又平面，则.

（2）解：由（1）知，，，两两相互垂直，

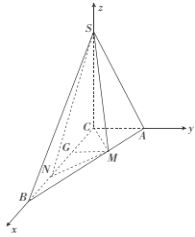
如图是以为坐标原点，分别以，，为轴，轴，轴的正方向建立空间直角坐标系，

则，，，，，

，，.

设平面的法向量为，则

，令，得.

设平面的法向量为，

则，令，则，，故.

所以，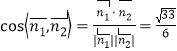

由图可知二面角为钝角，

故二面角的余弦值为.